题目内容
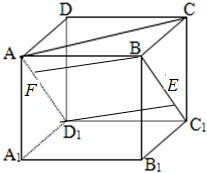 如图所示,棱长为1的正方体ABCD-A1B1C1D1中,E、F是侧面对角线BC1、AD1上一点,若BED1F是菱形,则BED1F在底面ABCD上投影四边形的面积是多少?
如图所示,棱长为1的正方体ABCD-A1B1C1D1中,E、F是侧面对角线BC1、AD1上一点,若BED1F是菱形,则BED1F在底面ABCD上投影四边形的面积是多少?考点:平行投影及平行投影作图法
专题:空间位置关系与距离
分析:设AF=x,结合菱形的边长相等及勾股定理,可得菱形BED1F的边长为
,进而可得BED1F在底面ABCD上投影四边形是底边为
,高为1的平行四边形.
| 3 |
| 4 |
| 2 |
| 3 |
| 4 |
解答:
解:在棱长为1的正方体ABCD-A1B1C1D1中,
BC1=AD1=
,
设AF=x,则
-x=
,
解得:x=
,
即菱形BED1F的边长为
-
=
,
则BED1F在底面ABCD上投影四边形是底边为
,高为1的平行四边形,
其面积为:
.
BC1=AD1=
| 2 |
设AF=x,则
| 2 |
| 1+x2 |
解得:x=
| 1 |
| 4 |
| 2 |
即菱形BED1F的边长为
| 2 |
| 1 |
| 4 |
| 2 |
| 3 |
| 4 |
| 2 |
则BED1F在底面ABCD上投影四边形是底边为
| 3 |
| 4 |
其面积为:
| 3 |
| 4 |
点评:本题考查的知识点是平行投影,其中分析出BED1F在底面ABCD上投影四边形是底边为
,高为1的平行四边形,是解答的关键.
| 3 |
| 4 |

练习册系列答案
相关题目
甲、乙两个同学分别解一道一元二次方程,甲因把一次项系数看错了,而解得方程两根为-3和5,乙把常数项看错了,解得两根为2+
和2-
,则原方程是( )
| 6 |
| 6 |
| A、x2+4x-15=0 |
| B、x2-4x+15=0 |
| C、x2+4x+15=0 |
| D、x2-4x-15=0 |
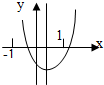 已知二次函数f(x)=ax2+bx+c(a≠0)的图象如图所示,设M=|a+b+c|-|a-b+c|+|2a+b|-|2a-b,则( )
已知二次函数f(x)=ax2+bx+c(a≠0)的图象如图所示,设M=|a+b+c|-|a-b+c|+|2a+b|-|2a-b,则( )| A、M>0 | B、M≥0 |
| C、M<0 | D、M=0 |