题目内容
若sin(π-α)=
,则cos(π+α)= .
| 1 |
| 3 |
考点:运用诱导公式化简求值,同角三角函数基本关系的运用
专题:计算题,三角函数的求值
分析:由sin(π-α)=
可解得sinα=
,从而有cos(π+α)=-cosα=±
=±
=±
.
| 1 |
| 3 |
| 1 |
| 3 |
| 1-sin2α |
1-
|
2
| ||
| 3 |
解答:
解:∵sin(π-α)=
,∴sinα=
,
∴cos(π+α)=-cosα=±
=±
=±
故答案为:±
| 1 |
| 3 |
| 1 |
| 3 |
∴cos(π+α)=-cosα=±
| 1-sin2α |
1-
|
2
| ||
| 3 |
故答案为:±
2
| ||
| 3 |
点评:本题主要考察了运用诱导公式化简求值,同角三角函数基本关系的运用,属于基础题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
复数z=
的虚部为( )
| 2 |
| 1+i |
| A、1 | B、-1 | C、i | D、-i |

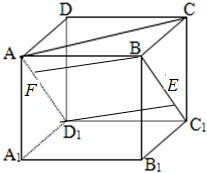 如图所示,棱长为1的正方体ABCD-A1B1C1D1中,E、F是侧面对角线BC1、AD1上一点,若BED1F是菱形,则BED1F在底面ABCD上投影四边形的面积是多少?
如图所示,棱长为1的正方体ABCD-A1B1C1D1中,E、F是侧面对角线BC1、AD1上一点,若BED1F是菱形,则BED1F在底面ABCD上投影四边形的面积是多少?