题目内容
已知圆C与x轴交于A(-1,0)和B(3,0),与y轴交于点M(0,3).
(1)求△ABM的面积;
(2)求线段AM的垂直平分线l的方程,并化为一般式;
(3)求圆C的方程;
(4)判别直线3x+4y+7=0与圆C的位置关系.
(1)求△ABM的面积;
(2)求线段AM的垂直平分线l的方程,并化为一般式;
(3)求圆C的方程;
(4)判别直线3x+4y+7=0与圆C的位置关系.
考点:圆的标准方程,直线的一般式方程,直线与圆的位置关系
专题:直线与圆
分析:(1)由题意可得,△ABM的面积为
|AB|•yM,计算求得结果.
(2)求得线段AM的中点坐标以及AM的斜率,可得AM的垂直平分线l的斜率,再利用点斜式求得线段AM的垂直平分线l的方程,再化为一般式.
(3)根据直线和圆相交的性质可得圆心C在线段AB的中垂线x=1上,设圆心C(1,b),则由|CA|=|CM|求得b=1,可得圆心C的坐标和半径|CA|的值,从而求得圆的方程.
(4)求得圆心C(1,1)到直线3x+4y+7=0的距离大于半径,可得直线和圆相离.
| 1 |
| 2 |
(2)求得线段AM的中点坐标以及AM的斜率,可得AM的垂直平分线l的斜率,再利用点斜式求得线段AM的垂直平分线l的方程,再化为一般式.
(3)根据直线和圆相交的性质可得圆心C在线段AB的中垂线x=1上,设圆心C(1,b),则由|CA|=|CM|求得b=1,可得圆心C的坐标和半径|CA|的值,从而求得圆的方程.
(4)求得圆心C(1,1)到直线3x+4y+7=0的距离大于半径,可得直线和圆相离.
解答:
解:(1)△ABM的面积为
|AB|•yM=
•4•3=6.
(2)由于线段AM的中点为(-
,
),且AM的斜率为
=3,故AM的垂直平分线l的斜率为-
,
故线段AM的垂直平分线l的方程为 y-
=-
(x+
),化为一般式为x+3y-4=0.
(3)根据直线和圆相交的性质可得圆心C在线段AB的中垂线x=1上,设圆心C(1,b),
则由|CA|=|CM|可得22+b2=11+(b-3)2,求得b=1,故圆心C(1,1)、半径为|CA|=
,
故圆的方程为 (x-1)2+(y-1)2=5.
(4)由于圆心C(1,1)到直线3x+4y+7=0的距离为
=
>
,
故直线和圆相离.
| 1 |
| 2 |
| 1 |
| 2 |
(2)由于线段AM的中点为(-
| 1 |
| 2 |
| 3 |
| 2 |
| 3-0 |
| 0+1 |
| 1 |
| 3 |
故线段AM的垂直平分线l的方程为 y-
| 3 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
(3)根据直线和圆相交的性质可得圆心C在线段AB的中垂线x=1上,设圆心C(1,b),
则由|CA|=|CM|可得22+b2=11+(b-3)2,求得b=1,故圆心C(1,1)、半径为|CA|=
| 5 |
故圆的方程为 (x-1)2+(y-1)2=5.
(4)由于圆心C(1,1)到直线3x+4y+7=0的距离为
| |3+4+7| |
| 5 |
| 14 |
| 5 |
| 5 |
故直线和圆相离.
点评:本题主要考查用点斜式求直线的方程,求圆的标准方程,直线和圆的位置关系的判定,属于基础题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
复数z=
的虚部为( )
| 2 |
| 1+i |
| A、1 | B、-1 | C、i | D、-i |
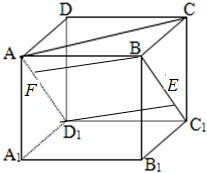 如图所示,棱长为1的正方体ABCD-A1B1C1D1中,E、F是侧面对角线BC1、AD1上一点,若BED1F是菱形,则BED1F在底面ABCD上投影四边形的面积是多少?
如图所示,棱长为1的正方体ABCD-A1B1C1D1中,E、F是侧面对角线BC1、AD1上一点,若BED1F是菱形,则BED1F在底面ABCD上投影四边形的面积是多少? 如图,已知P是平行四边形ABCD所在平面外一点,M、N分别是AB、PC的中点;
如图,已知P是平行四边形ABCD所在平面外一点,M、N分别是AB、PC的中点;