题目内容
已知π<θ<2π,sin(
+θ)=-
,则tan(π+θ)的值为 .
| π |
| 2 |
| 3 |
| 5 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:直接利用诱导公式化简已知条件,化简所求的表达式,通过同角三角函数的基本关系式求解即可.
解答:
解:π<θ<2π,sin(
+θ)=-
,
可得cosθ=
,sinθ=-
=-
,∴tanθ=
=-
.
∴tan(π+θ)=tanθ=-
.
故答案为:-
.
| π |
| 2 |
| 3 |
| 5 |
可得cosθ=
| 3 |
| 5 |
| 1-cos2θ |
| 4 |
| 5 |
| sinθ |
| cosθ |
| 4 |
| 3 |
∴tan(π+θ)=tanθ=-
| 4 |
| 3 |
故答案为:-
| 4 |
| 3 |
点评:本题考查诱导公式的应用,三角函数的化简求值,基本知识的考查.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
阅读图中的程序:

图中程序在执行过程中,如果输入6,那么输出的结果是( )

图中程序在执行过程中,如果输入6,那么输出的结果是( )
| A、6 | B、120 |
| C、720 | D、1080 |
复数z=
的虚部为( )
| 2 |
| 1+i |
| A、1 | B、-1 | C、i | D、-i |
函数y=
+
的值域是( )
| ||
| cosx |
| ||
| sinx |
| A、{0,2} |
| B、{-2,2} |
| C、{0,-2} |
| D、{-2,0,2} |
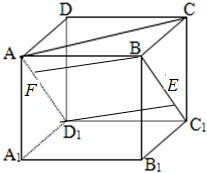 如图所示,棱长为1的正方体ABCD-A1B1C1D1中,E、F是侧面对角线BC1、AD1上一点,若BED1F是菱形,则BED1F在底面ABCD上投影四边形的面积是多少?
如图所示,棱长为1的正方体ABCD-A1B1C1D1中,E、F是侧面对角线BC1、AD1上一点,若BED1F是菱形,则BED1F在底面ABCD上投影四边形的面积是多少?