题目内容

函数f（x）=ax3+bx+2，若f（2）=3，则f（-2）的值等于
 
．
考点：函数的值
专题：函数的性质及应用
分析：由已知得f（2）=8a+2b+2=3，由此能求出f（-2）=-8a-2b+2的值．
解答： 解：∵f（x）=ax3+bx+2，f（2）=3，
∴f（2）=8a+2b+2=3，
解得8a+2b=1，
∴f（-2）=-8a-2b+2
=-1+2=1．
故答案为：1．
点评：本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．
练习册系列答案
相关题目
△ABC中内角A、B、C的对边分别是a、b、c．若a2-c2=
3
bc，sinB=2
3
sinC，则A=（　　）
A、
5
6
π
B、
2
3
π
C、
π
3
D、
π
6
复数Z=cosθ+isinθ（θ∈（0，2π））在复平面上所对应的点在第二象限上，则θ的取值范围是
 
．
设函数f（x）=
x2+2(x≤2)
2x(x＞2)
，则f（f（1））=
 
．
阅读图中的程序：

图中程序在执行过程中，如果输入6，那么输出的结果是（　　）
A、6B、120
C、720D、1080
已知函数f（x）=2x-kxa-2（k，a∈R）的图象经过点（1，0），设g（x）=
f(x)，x≤0
log2(x+1)，x＞0
，若g（t）=2，则实数t的值为（　　）
A、3B、-3C、3D、2或3
执行如图所示的程序框图，输出结果y的值是
 
．
已知sin（π+α）=
3
5
，α∈(-
π
2
，0)，则tanα=
 
．
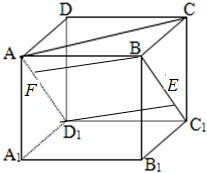如图所示，棱长为1的正方体ABCD-A1B1C1D1中，E、F是侧面对角线BC1、AD1上一点，若BED1F是菱形，则BED1F在底面ABCD上投影四边形的面积是多少？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网