题目内容
19.下列命题:(1)“若am2≥bm2,则a≥b”的否命题;
(2)“全等三角形面积相等”的逆命题;
(3)“若a>1,则关于x的不等式ax2≥0的解集为R”的逆否命题;
其中正确命题的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据四种命题的定义,写出对应的命题,可判断(1)(2),根据互为逆否的两个命题真假性相同,可判断(3).
解答 解:(1)“若am2≥bm2,则a≥b”的否命题为“若am2<bm2,则a<b”为真命题,故(1)正确;
(2)“全等三角形面积相等”的逆命题为“面积相等的三角形全等”为假命题,故(2)错误;
(3)“若a>1,则关于x的不等式ax2≥0的解集为R”为真命题,其逆否命题也为真命题,故(3)正确;
故选:B.
点评 本题以命题的真假判断与应用为载体,考查了四种命题,不等式的性质,难度中档.

练习册系列答案
相关题目
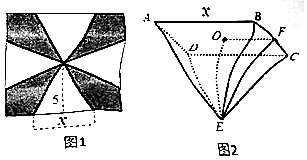
14.将一块边长为10的正方形铁片按图1所示的阴影部分裁下,用余下的四个全等的等腰三角形加工成一个底面边长为x的正四棱锥形容器(如图2),则函数f(x)=$\frac{{V}_{E-ABCD}}{x}$的最大值为( )

| A. | $\frac{25\sqrt{3}}{6}$ | B. | $\frac{50}{3}$ | C. | $\frac{25}{3}$ | D. | $\frac{125\sqrt{3}}{6}$ |
4.在△ABC中,$AC=\sqrt{7},BC=2,B=60°$,则BC边上的高为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{3\sqrt{3}}}{2}$ | D. | $\sqrt{6}$ |
11.已知球面上的四点P、A、B、C,PA、PB、PC的长分别为3、4、5,且这三条线段两两垂直,则这个球的体积为( )
| A. | $\frac{{1000\sqrt{2}}}{3}π$ | B. | $\frac{{375\sqrt{2}}}{16}π$ | C. | 50π | D. | $\frac{{125\sqrt{2}}}{3}π$ |
8.空间的一个基底{a,b,c}所确定平面的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个以上 |