题目内容
4.函数f(x)=$\frac{1}{\sqrt{lo{g}_{\frac{1}{2}}x}}$的定义域为(0,1).分析 要使函数有意义,则需x>0,且$lo{g}_{\frac{1}{2}}x>0$,运用对数函数的单调性求解,即可得到定义域.
解答 解:由题意得:$\left\{\begin{array}{l}{x>0}\\{lo{g}_{\frac{1}{2}}x>0}\end{array}\right.$,
解得:0<x<1.
∴函数f(x)=$\frac{1}{\sqrt{lo{g}_{\frac{1}{2}}x}}$的定义域为:(0,1).
故答案为:(0,1).
点评 本题考查函数的定义域的求法,注意偶次根式被开方式非负,对数的真数大于0,分式的分母不等于0,属于基础题.

练习册系列答案
相关题目
19.已知直线的斜率是6,在y轴上的截距是-4,则此直线方程是( )
| A. | 6x-y-4=0 | B. | 6x-y+4=0 | C. | 6x+y+4=0 | D. | 6x+y-4=0 |
9.一个年级有12个班,每个班有50名学生,随机编号为1~50,为了了解他们课外的兴趣,要求每班第40号学生留下来进行问卷调查,这运用的抽样方法是( )
| A. | 分层抽样 | B. | 抽签法 | C. | 随机数表法 | D. | 系统抽样法 |
8.空间的一个基底{a,b,c}所确定平面的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个以上 |
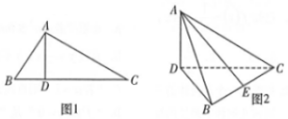 如图1,在Rt△ABC中,∠ABC=60°,AD是斜边BC上的高,沿AD将△ABC折成60°的二面角B-AD-C,如图2.
如图1,在Rt△ABC中,∠ABC=60°,AD是斜边BC上的高,沿AD将△ABC折成60°的二面角B-AD-C,如图2.