题目内容
3.已知函数f(x)=$\left\{\begin{array}{l}{{e}^{x},x≤0}\\{{x}^{2}+ax+1,x>0}\end{array}\right.$,F(x)=f(x)-x-1,且函数F(x)有2个零点,则实数a的取值范围为( )| A. | (一∞,0] | B. | [1,+∞) | C. | (一∞,1) | D. | (0,+∞) |
分析 作出函数的图象,x≤0,F(x)=ex-x-1,有一个零点0,x>0,F(x)=x[x+(a-1)],0是其中一个零点,利用函数F(x)有2个零点,可得1-a>0,即可求出实数a的取值范围.
解答  解:由题意,x≤0,F(x)=ex-x-1,有一个零点0,
解:由题意,x≤0,F(x)=ex-x-1,有一个零点0,
x>0,F(x)=x[x+(a-1)],0是其中一个零点,
∵函数F(x)有2个零点,
∴1-a>0,∴a<1.
故选C.
点评 本题考查函数的零点,考查数形结合的数学思想,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
19.已知直线的斜率是6,在y轴上的截距是-4,则此直线方程是( )
| A. | 6x-y-4=0 | B. | 6x-y+4=0 | C. | 6x+y+4=0 | D. | 6x+y-4=0 |
14.将一块边长为10的正方形铁片按图1所示的阴影部分裁下,用余下的四个全等的等腰三角形加工成一个底面边长为x的正四棱锥形容器(如图2),则函数f(x)=$\frac{{V}_{E-ABCD}}{x}$的最大值为( )
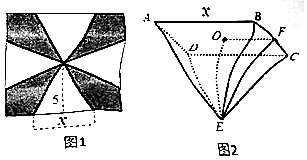

| A. | $\frac{25\sqrt{3}}{6}$ | B. | $\frac{50}{3}$ | C. | $\frac{25}{3}$ | D. | $\frac{125\sqrt{3}}{6}$ |
11.已知球面上的四点P、A、B、C,PA、PB、PC的长分别为3、4、5,且这三条线段两两垂直,则这个球的体积为( )
| A. | $\frac{{1000\sqrt{2}}}{3}π$ | B. | $\frac{{375\sqrt{2}}}{16}π$ | C. | 50π | D. | $\frac{{125\sqrt{2}}}{3}π$ |
8.空间的一个基底{a,b,c}所确定平面的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个以上 |