题目内容
在△ABC中，已知为
=
，求
．
| 2cosA-3sinC |
| cosB |
| 3c-2a |
| b |
| a |
| c |
考点：余弦定理
专题：解三角形
分析：利用正弦定理及其
=
，可得
=
，化简整理可得2sinC=3sinA，即可得出．
| 2cosA-3sinC |
| cosB |
| 3c-2a |
| b |
| 2cosA-3cosC |
| cosB |
| 3sinC-2sinA |
| sinB |
解答：
解：由正弦定理
=
=
═2R得：a=2RsinA；b=2RsinB；c=2RsinC，
∴
=
，
即2cosA•sinB-3sinB•cosC=3cosB•sinC-2sinAcosB，
整理得：2（sinAcosB+cosA•sinB）=3（sinB•cosC+cosB•sinC），
即2sin（A+B）=3sin（B+C），
∵A+B=π-C；B+C=π-A，
∴2sin（π-C）=3sin（π-A），
即2sinC=3sinA，
∴
=
=
．
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
∴
| 2cosA-3cosC |
| cosB |
| 3sinC-2sinA |
| sinB |
即2cosA•sinB-3sinB•cosC=3cosB•sinC-2sinAcosB，
整理得：2（sinAcosB+cosA•sinB）=3（sinB•cosC+cosB•sinC），
即2sin（A+B）=3sin（B+C），
∵A+B=π-C；B+C=π-A，
∴2sin（π-C）=3sin（π-A），
即2sinC=3sinA，
∴
| a |
| c |
| sinA |
| sinC |
| 2 |
| 3 |
点评：本题考查了正弦定理、两角和差的正弦公式、三角形的内角和定理、诱导公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
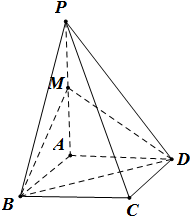如图，在四棱锥P-ABCD中，底面ABCD是边长为1的菱形，∠ABC=| π |
| 3 |
（Ⅰ）求证：直线PC∥平面MBD；
（Ⅱ）求异面直线AB与MD所成角的余弦值．
在△ABC中，若sin2A+sin2C+cos2B＜1，则△ABC一定是（ ）
| A、钝角三角形 | B、直角三角形 |
| C、锐角三角形 | D、不确定 |
如图，D是△ABC的边AB的中点，则向量
=（ ）
| CD |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|