题目内容
函数y=x（4-x）（0＜x＜4）的最大值为 ．
考点：二次函数的性质
专题：函数的性质及应用
分析：根据函数y=f（x）的图象与性质，求出0＜x＜4时，f（x）的最大值即可．
解答：
解：∵函数y=f（x）=x（4-x）=4x-x2=-（x-2）2+4，
当0＜x＜4时，y的最大值为y=f（2）=4．
故答案为：4．
当0＜x＜4时，y的最大值为y=f（2）=4．
故答案为：4．
点评：本题考查了二次函数在某一区间上的最值问题，是基础题目．
练习册系列答案
相关题目
定义在实数集R上的函数y=f（x）的图象是连续不断的，若对任意的实数x，存在不为0的常数r使得f（x+r）=-rf（x）恒成立，则称f（x）是一个“关于r函数”，下列“关于r函数”的结论正确的是（ ）
| A、f（x）=0是常数函数中唯一一个“关于r函数” | ||
| B、f（x）=x2是一个“关于r函数” | ||
| C、f（x）=sinπx不是一个“关于r函数” | ||
D、“关于
|
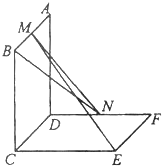如图，已知两个正方形ABCD 和DCEF不在同一平面内，且平面ABCD⊥平面DCEF，M，N分别为AB，DF的中点．
在正方体ABCD-A1B1C1D1中，P，Q分别是AB，B1C1上的点AP=B1Q，N是PQ的中点，M是正方形ABB1A1的中心．求证：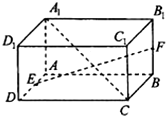
如图，在长方体ABCD-A1B1C1D1中，AB=4，AD=AA1=2，点E、F分别是AD、BB1的中点．