题目内容
设函数f(x)=mx2-(4+m2)x,其中m∈R,且m>0,区间D={x|f(x)<0}.
(1)求区间D的长度(区间(a,b)的长度定义为b-a);
(2)记区间D的长度为g(m),试用函数的单调性定义证明g(m)在(0,2)上单调递减,在(2,+∞)上单调递增;
(3)给定常数t∈(0,2),当2-t≤m≤2+t时,求区间D的长度的最大值.
(1)求区间D的长度(区间(a,b)的长度定义为b-a);
(2)记区间D的长度为g(m),试用函数的单调性定义证明g(m)在(0,2)上单调递减,在(2,+∞)上单调递增;
(3)给定常数t∈(0,2),当2-t≤m≤2+t时,求区间D的长度的最大值.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)解不等式mx2-(4+m2)x<0,m<0,即可得出0<x<
,求出b-a=
,
(2)区间D的长度为g(m)=
=m+
,运用单调性的定义证明.
(3)判断当m=2时,g(m)=4,此时为最小值
当m=t-2时,g(2-t)=2-t+
,当m=t+2时,g(t+2)=t+2+
,作差g(t+2)-g(2-t)=2t+
-
=2t+
=
<0,即可得出区间D的长度的最大值为g(2-t).
| m2+4 |
| m |
| m2+4 |
| m |
(2)区间D的长度为g(m)=
| m2+4 |
| m |
| 4 |
| m |
(3)判断当m=2时,g(m)=4,此时为最小值
当m=t-2时,g(2-t)=2-t+
| 4 |
| 2-t |
| 4 |
| t+2 |
| 4 |
| t+2 |
| 4 |
| 2-t |
| -8t |
| 4-t2 |
| -2t3 |
| 4-t2 |
解答:
解:(1)∵函数f(x)=mx2-(4+m2)x,其中m∈R,且m>0,区间D={x|f(x)<0}.
∴区间D={x|f(x)<0}.
∵mx2-(4+m2)x<0,m<0,
∴mx2-(4+m2)x=0,
x=0,x=
,
∴0<x<
,
b-a=
,
(2)区间D的长度为g(m)=
=m+
,
m1<m2,g(m1)-g(m2))=m1+
-m2-
=(m1-m2)
,
∵m1,m2∈(0,2),
∴m1-m2<0,0<m1m2<4,
∴m1m2-4<0,
∴g(m1)-g(m2))>0,
∴g(m)在(0,2)上单调递减,
∵m1,m2∈(2,+∞)
∴m1m2>4,m1-m2<0,m1m2-4>0,
∴g(m1)-g(m2))<0,
g(m)在(2,+∞)上单调递增;
(3)∵区间D的长度为g(m)=
=m+
,给定常数t∈(0,2),当2-t≤m≤2+t时,
∴2∈(2-t,2+t),(2-t,2)单调递减,(2,2+t)单调递增,
当m=2时,g(m)=4,此时为最小值
当m=t-2时,g(2-t)=2-t+
,
当m=t+2时,g(t+2)=t+2+
,
∵g(t+2)-g(2-t)=2t+
-
=2t+
=
<0,
∴g(t+2)<g(2-t),
区间D的长度的最大值为g(2-t).
∴区间D={x|f(x)<0}.
∵mx2-(4+m2)x<0,m<0,
∴mx2-(4+m2)x=0,
x=0,x=
| m2+4 |
| m |
∴0<x<
| m2+4 |
| m |
b-a=
| m2+4 |
| m |
(2)区间D的长度为g(m)=
| m2+4 |
| m |
| 4 |
| m |
m1<m2,g(m1)-g(m2))=m1+
| 4 |
| m1 |
| 4 |
| m2 |
| (m1m2-4) |
| m1m2 |
∵m1,m2∈(0,2),
∴m1-m2<0,0<m1m2<4,
∴m1m2-4<0,
∴g(m1)-g(m2))>0,
∴g(m)在(0,2)上单调递减,
∵m1,m2∈(2,+∞)
∴m1m2>4,m1-m2<0,m1m2-4>0,
∴g(m1)-g(m2))<0,
g(m)在(2,+∞)上单调递增;
(3)∵区间D的长度为g(m)=
| m2+4 |
| m |
| 4 |
| m |
∴2∈(2-t,2+t),(2-t,2)单调递减,(2,2+t)单调递增,
当m=2时,g(m)=4,此时为最小值
当m=t-2时,g(2-t)=2-t+
| 4 |
| 2-t |
当m=t+2时,g(t+2)=t+2+
| 4 |
| t+2 |
∵g(t+2)-g(2-t)=2t+
| 4 |
| t+2 |
| 4 |
| 2-t |
| -8t |
| 4-t2 |
| -2t3 |
| 4-t2 |
∴g(t+2)<g(2-t),
区间D的长度的最大值为g(2-t).
点评:本题考查了二次函数的性质,单调性的定义,运用不等式求解问题,属于中档题.

练习册系列答案
相关题目
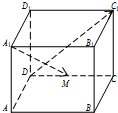 如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,M是棱CD的中点,则
如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,M是棱CD的中点,则| A1M |
| DC1 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
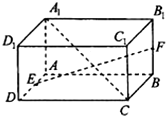 如图,在长方体ABCD-A1B1C1D1中,AB=4,AD=AA1=2,点E、F分别是AD、BB1的中点.
如图,在长方体ABCD-A1B1C1D1中,AB=4,AD=AA1=2,点E、F分别是AD、BB1的中点.



