题目内容
某厂生产某种零件,每个零件的成本为40元,出厂单价为60元,该厂为鼓励销售商,决定当一次性订购量不少于100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂单价不能低于50元(例如一次性订购101个零件,则101个零件的单价是60-1×0.02=59.98元).
(1)当销售商一次订购500个零件时,该厂获得的利润是多少元?
(2)设一次订购量为X个时,零件的出厂单价为Y元.写出y=f(X)的函数表达式;
(3)若厂方现有600个零件,当销售商一次性订购量x(x>100)为多少个时,厂方的销售额g(x)最大?(销售额g(x)=销售数量×销售单价)
(1)当销售商一次订购500个零件时,该厂获得的利润是多少元?
(2)设一次订购量为X个时,零件的出厂单价为Y元.写出y=f(X)的函数表达式;
(3)若厂方现有600个零件,当销售商一次性订购量x(x>100)为多少个时,厂方的销售额g(x)最大?(销售额g(x)=销售数量×销售单价)
考点:函数与方程的综合运用,二次函数的性质
专题:计算题,应用题,函数的性质及应用
分析:(1)由题意,实际出厂单价为60-(500-100)×0.02=52元,
(2)利用分段函数写出函数解析式即可,
(3)化简g(x)=x[60-0.02(x-100)]=-0.02x2+62x,从而利用二次函数求最值即可.
(2)利用分段函数写出函数解析式即可,
(3)化简g(x)=x[60-0.02(x-100)]=-0.02x2+62x,从而利用二次函数求最值即可.
解答:
解(1)当销售商一次订购500个零件时,
实际出厂单价为60-(500-100)×0.02=52元,
故该厂获得的利润为y=500×(52-40)=6000元;
(2)由题意,
y=
,X∈N*,
(3)由(2)知,
g(x)=x[60-0.02(x-100)]
=-0.02x2+62x
故当x=600时,g(x)有最大值,
gmax(x)=g(600)=30000(元);
即当当销售商一次性订购量为600个时,厂方的销售额g(x)最大.
实际出厂单价为60-(500-100)×0.02=52元,
故该厂获得的利润为y=500×(52-40)=6000元;
(2)由题意,
y=
|
(3)由(2)知,
g(x)=x[60-0.02(x-100)]
=-0.02x2+62x
故当x=600时,g(x)有最大值,
gmax(x)=g(600)=30000(元);
即当当销售商一次性订购量为600个时,厂方的销售额g(x)最大.
点评:本题考查了函数在实际问题中的应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数y=x2-x+2在下列哪个区间上是单调减函数( )
| A、(0,+∞) |
| B、(-∞,0) |
| C、(1,+∞) |
| D、(-∞,1) |
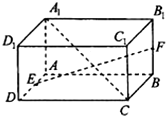 如图,在长方体ABCD-A1B1C1D1中,AB=4,AD=AA1=2,点E、F分别是AD、BB1的中点.
如图,在长方体ABCD-A1B1C1D1中,AB=4,AD=AA1=2,点E、F分别是AD、BB1的中点.



