题目内容

3．执行如所示程序框图所表达的算法，输出的结果是 （　　）
A．80B．99C．116D．120

分析 由图知，每次进入循环体后，新的s值是s加上2n+1得到的，故由此运算规律进行计算，经过8次运算后输出的结果即可．

解答 解：由图知s的运算规则是：s=s+（2n+1），故有：
第一次进入循环体后s=3，n=2，
第二次进入循环体后s=3+5，n=3，
第三次进入循环体后s=3+5+7，n=4，
第四次进入循环体后s=3+5+7+9，n=5，
…
第10次进入循环体后s=3+5+7+9+…+17，n=9．
由于n=9＞8，退出循环．
故该程序运行后输出的结果是：s=3+5+7+9+…+17=80．
故选：A．

点评 本题考查循环结构，已知运算规则与运算次数，求最后运算结果的一个题，是算法中一种常见的题型，属于基础题．

练习册系列答案
相关题目
13．经过点P（0，-1）作直线l，若直线l与连接A（1，-2），B（2，1）的线段没有公共点，则直线l的斜率k与倾斜角α的取值范围分别是（　　）
A．（-∞，-1）∪（1，+∞），（$\frac{π}{4}$，$\frac{3π}{4}$）B．（-∞，-1）∪（1，+∞），（$\frac{π}{4}$，$\frac{π}{2}$）∪（$\frac{π}{2}$，$\frac{3π}{4}$）
C．（-1，1），[$\frac{π}{4}$，$\frac{3π}{4}$]D．（-1，1），[0，$\frac{π}{4}$]∪[$\frac{3π}{4}$，0）
14．幂函数y=x3在[1，2]上的最大值与最小值之和为（　　）
A．10B．9C．8D．6
11．已知|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=2，＜$\overrightarrow{a}$，$\overrightarrow{b}$＞=60°，则|$\overrightarrow{a}$-$\overrightarrow{b}$|=（　　）
A．1B．2C．$\sqrt{3}$D．4
18．若a为实数，且$\frac{2-ai}{1+i}=3+i$，则a=（　　）
A．-4B．-3C．3D．4
8．执行如图所示的程序框图，输出S的值是（　　）
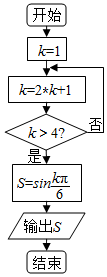
A．$\frac{{\sqrt{3}}}{2}$B．$-\frac{{\sqrt{3}}}{2}$C．$\frac{1}{2}$D．$-\frac{1}{2}$
15．已知a，b，c为互不相等的整数，则4（a2+b2+c2）-（a+b+c）2的最小值为8．
12．算法程序框图如图所示，若$a=\frac{π}{2}$，$b={3^{\frac{1}{3}}}$，$c={（{\sqrt{e}}）^{ln3}}$，则输出的结果是（　　）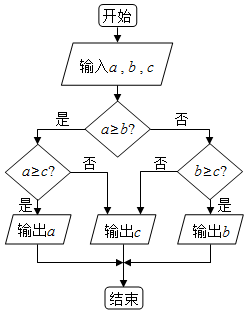
A．$\frac{a+b+c}{3}$B．aC．bD．c
13．已知函数f（x）=$\left\{\begin{array}{l}{\sqrt{1+9{x}^{2}，}}&{x≤0}\\{1+x{e}^{x-1}，}&{x＞0}\end{array}\right.$，点A、B是函数f（x）图象上不同两点，则∠AOB（O为坐标原点）的取值范围是（　　）
A．（0，$\frac{π}{4}$）B．（0，$\frac{π}{4}$]C．（0，$\frac{π}{3}$）D．（0，$\frac{π}{3}$]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网