题目内容
13.经过点P(0,-1)作直线l,若直线l与连接A(1,-2),B(2,1)的线段没有公共点,则直线l的斜率k与倾斜角α的取值范围分别是( )| A. | (-∞,-1)∪(1,+∞),($\frac{π}{4}$,$\frac{3π}{4}$) | B. | (-∞,-1)∪(1,+∞),($\frac{π}{4}$,$\frac{π}{2}$)∪($\frac{π}{2}$,$\frac{3π}{4}$) | ||
| C. | (-1,1),[$\frac{π}{4}$,$\frac{3π}{4}$] | D. | (-1,1),[0,$\frac{π}{4}$]∪[$\frac{3π}{4}$,0) |
分析 由题意画出图形,数形结合求出使直线l与线段AB有公共点的直线l的斜率的范围与倾斜角的范围,然后利用补集思想得答案.
解答 解:如图,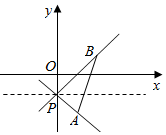
∵A(1,-2),B(2,1),P(0,-1),
∴${k}_{PA}=\frac{-2-(-1)}{1-0}=-1$,${k}_{PB}=\frac{-1-1}{-0-2}=1$,
则使直线l与线段AB有公共点的直线l的斜率的范围为[-1,1],倾斜角的范围为[0,$\frac{π}{4}$]∪[$\frac{3π}{4},π$).
由补集思想可得,直线l与连接A,B的线段没有公共点的斜率的范围为(-∞,-1)∪(1,+∞),
直线的倾斜角的范围为($\frac{π}{4}$,$\frac{3π}{4}$).
故选:A.
点评 本题考查直线的倾斜角,考查了直线的倾斜角和斜率的关系,体现了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
1.若复数z满足:iz=i+z,则z=( )
| A. | 1+i | B. | 1-i | C. | $\frac{1+i}{2}$ | D. | $\frac{1-i}{2}$ |
2.某初级中学有学生111人,其中一年级108人,二、三年级各81人,现要利用抽样方法取10人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为1,2,…,270;使用系统抽样时,将学生统一随机编号1,2,…,270,并将整个编号依次分为10段 如果抽得号码有下列四种情况:
①7,34,61,88,115,142,169,196,223,250;
②5,9,100,107,111,121,180,195,200,265;
③11,38,65,92,119,146,173,200,227,254;
④30,57,84,111,138,165,192,219,246,270;
关于上述样本的下列结论中,正确的是( )
①7,34,61,88,115,142,169,196,223,250;
②5,9,100,107,111,121,180,195,200,265;
③11,38,65,92,119,146,173,200,227,254;
④30,57,84,111,138,165,192,219,246,270;
关于上述样本的下列结论中,正确的是( )
| A. | ②、③都不能为系统抽样 | B. | ②、④都不能为分层抽样 | ||
| C. | ①、③都可能为分层抽样 | D. | ①、④都可能为系统抽样 |
3.执行如所示程序框图所表达的算法,输出的结果是 ( )


| A. | 80 | B. | 99 | C. | 116 | D. | 120 |
