题目内容
8.执行如图所示的程序框图,输出S的值是( )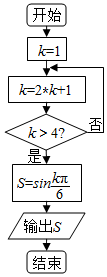
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
分析 分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是利用循环计算k的值,计算S=sin$\frac{kπ}{6}$的值并输出,模拟程序的运行过程,即可得到答案.
解答 解:模拟执行程序,可得
k=1,
k=2×1+1=3,不满足条件k>4,
执行循环体,k=2×3+1=7,满足条件k>4,
∴$S=sin\frac{7π}{6}=-\frac{1}{2}$,
输出S的值为-$\frac{1}{2}$.
故选:D.
点评 本题主要考查了循环结构的程序框图,解决程序框图中的循环结构时,常采用按照流程写出前几次循环的结果,找规律,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.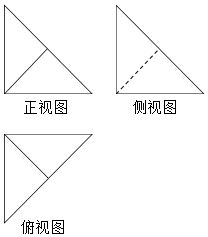 在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为正方形,PA=AB,该四棱锥被一平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )
在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为正方形,PA=AB,该四棱锥被一平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )
 在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为正方形,PA=AB,该四棱锥被一平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )
在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为正方形,PA=AB,该四棱锥被一平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
3.执行如所示程序框图所表达的算法,输出的结果是 ( )


| A. | 80 | B. | 99 | C. | 116 | D. | 120 |
13.已知t>0,函数f(x)=2x-1+$\sqrt{4+t-2tx}$的最大值为g(t),则g(t)的最小值为( )
| A. | 2 | B. | $\frac{\sqrt{2}}{4}$ | C. | 1 | D. | 2$\sqrt{2}$ |
20.函数f(x)=cos(ωx+φ)的部分图象如图所示,则下列结论成立的是( )
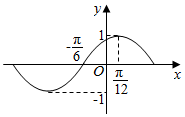

| A. | f(x)的递增区间是(2kπ-$\frac{5π}{12}$,2kπ+$\frac{π}{12}$),k∈Z | |
| B. | 函数f(x-$\frac{π}{3}$)是奇函数 | |
| C. | 函数f(x-$\frac{π}{12}$)是偶函数 | |
| D. | f(x)=cos(2x-$\frac{π}{6}$) |