题目内容
15.已知a,b,c为互不相等的整数,则4(a2+b2+c2)-(a+b+c)2的最小值为8.分析 设a+b+c=t,由于(a+b+c)2=a2+b2+c2+2ab+2bc+2ac,(a-b)2+(b-c)2+(a-c)2≥0,可得t2≤3(a2+b2+c2),4(a2+b2+c2)-(a+b+c)2≥$\frac{4}{3}{t}^{2}$-t2=$\frac{1}{3}{t}^{2}$,利用a,b,c为互不相等的整数,由于已知a,b,c为互不相等的整数,由此可知:只要使得a2+b2+c2取得最小值即可.
解答 解:设a+b+c=t,
∵(a+b+c)2=a2+b2+c2+2ab+2bc+2ac,
(a-b)2+(b-c)2+(a-c)2≥0,
∴2(a2+b2+c2)≥2ab+2bc+2ac,
∴t2≤3(a2+b2+c2),
4(a2+b2+c2)-(a+b+c)2≥$\frac{4}{3}{t}^{2}$-t2=$\frac{1}{3}{t}^{2}$,
若a,b,c为相等的整数,则当a=b=c=0时,最小值为0.
由于已知a,b,c为互不相等的整数,由此可知:只要使得a2+b2+c2取得最小值即可,
于是对于a,b,c的取值,只要考查a,b,c∈{-1,0,1}的情况即可得出.
不妨取a=-1,b=0,c=1时,4(a2+b2+c2)-(a+b+c)2取得最小值8.
点评 本题考查了不等式的性质、基本不等式的性质、乘法公式,考查了分类讨论方法、推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
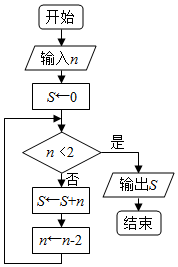
3.执行如所示程序框图所表达的算法,输出的结果是 ( )


| A. | 80 | B. | 99 | C. | 116 | D. | 120 |
20.函数f(x)=cos(ωx+φ)的部分图象如图所示,则下列结论成立的是( )
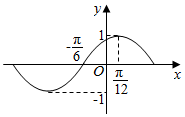

| A. | f(x)的递增区间是(2kπ-$\frac{5π}{12}$,2kπ+$\frac{π}{12}$),k∈Z | |
| B. | 函数f(x-$\frac{π}{3}$)是奇函数 | |
| C. | 函数f(x-$\frac{π}{12}$)是偶函数 | |
| D. | f(x)=cos(2x-$\frac{π}{6}$) |
5.已知不等式$\sqrt{(x-a)^{2}+4(lnx-a-\frac{1}{2})^{2}}$≥$\frac{3\sqrt{5}}{5}$恒成立,则实数a的取值为( )
| A. | $\frac{1}{5}$ | B. | -$\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{2}$ |