已知|$\overrightarrow{a}$|=1.|$\overrightarrow{b}$|=2.＜$\overrightarrow{a}$.$\overrightarrow{b}$＞=60°.则|$\overrightarrow{a}$-$\overrightarrow{b}$|=( )A．1B．2C．$\sqrt{3}$D．4 题目和参考答案——青夏教育精英家教网—

题目内容

11．已知|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=2，＜$\overrightarrow{a}$，$\overrightarrow{b}$＞=60°，则|$\overrightarrow{a}$-$\overrightarrow{b}$|=（　　）

A．

B．

C．

$\sqrt{3}$

D．

分析即（$\overrightarrow{a}-\overrightarrow{b}$）²，开方即为|$\overrightarrow{a}-\overrightarrow{b}$|．

解答解：$\overrightarrow{a}•\overrightarrow{b}$=1×2×cos60°=1，
∴（$\overrightarrow{a}-\overrightarrow{b}$）²=${\overrightarrow{a}}^{2}-2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}$=3，
∴|$\overrightarrow{a}-\overrightarrow{b}$|=$\sqrt{3}$．
故选：C．

点评本题考查了平面向量的数量积运算，属于基础题．

练习册系列答案

相关题目

1．若复数z满足：iz=i+z，则z=（　　）

2．某初级中学有学生111人，其中一年级108人，二、三年级各81人，现要利用抽样方法取10人参加某项调查，考虑选用简单随机抽样、分层抽样和系统抽样三种方案，使用简单随机抽样和分层抽样时，将学生按一、二、三年级依次统一编号为1，2，…，270；使用系统抽样时，将学生统一随机编号1，2，…，270，并将整个编号依次分为10段如果抽得号码有下列四种情况：
①7，34，61，88，115，142，169，196，223，250；
②5，9，100，107，111，121，180，195，200，265；
③11，38，65，92，119，146，173，200，227，254；
④30，57，84，111，138，165，192，219，246，270；
关于上述样本的下列结论中，正确的是（　　）

	A．	②、③都不能为系统抽样		B．	②、④都不能为分层抽样
	C．	①、③都可能为分层抽样		D．	①、④都可能为系统抽样

19．已知函数f（x）=sinx-$\frac{x}{2}$．当0＜x＜1时，不等式f（x）•log₂（x-2^m+$\frac{5}{4}$）＞0恒成立．则实数m得到取值范围是（-∞，-2]．

6．设a∈R，f（x）=|x-a|+（1-a）x．
（I）解关于a的不等式f（2）＜0；
（Ⅱ）如果f（x）≥0恒成立，求实数a的取值范围．

16．

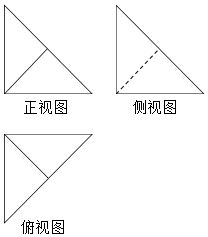在四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD为正方形，PA=AB，该四棱锥被一平面截去一部分后，剩余部分的三视图如图，则截去部分体积与剩余部分体积的比值为（　　）

3．执行如所示程序框图所表达的算法，输出的结果是（　　）

20．函数f（x）=cos（ωx+φ）的部分图象如图所示，则下列结论成立的是（　　）

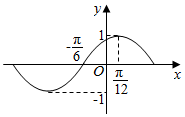
	A．	f（x）的递增区间是（2kπ-$\frac{5π}{12}$，2kπ+$\frac{π}{12}$），k∈Z
	B．	函数f（x-$\frac{π}{3}$）是奇函数
	C．	函数f（x-$\frac{π}{12}$）是偶函数
	D．	f（x）=cos（2x-$\frac{π}{6}$）

1．在长为2的线段AB上任意取一点C，以线段AC为半径的圆面积小于π的概率为（　　）

试题分类