Question

给出下列四个命题：
①命题“?x∈R，cosx＞0”的否定是“?x∈R，cosx≤0”；
②若0＜a＜1，则函数f（x）=x²+a^x-3只有一个零点；
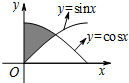
③函数y=sin（2x-

π

3

）的一个单调增区间是[-

π

12

，

5π

12

]；
④对于任意实数x，有f（-x）=f（x），且当x＞0时，f′（x）＞0，则当x＜0时，f′（x）＜0．
⑤若m∈（0，1]，则函数y=m+

3

m

的最小值为2

3

；
其中真命题的序号是

 

（把所有真命题的序号都填上）．

Answer 1

考点：命题的真假判断与应用

专题：简易逻辑

分析：①利用命题的否定形式判断即可；
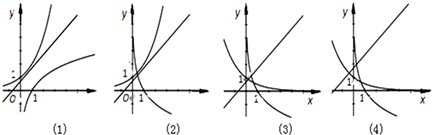
②利用y=a^x与y=3-x²的图象的交点个数判断即可；
③由-

π

2

≤2x-

π

3

≤

π

2

可求得函数y=sin（2x-

π

3

）的一个单调增区间，观察该区间是否包含区间[-

π

12

，

5π

12

]即可；
④利用偶函数在对称区间上单调性相反即可判断④的正误；
⑤利用双钩函数的单调性质判断即可．

解答： 解：①命题“?x∈R，cosx＞0”的否定是“?x∈R，cosx≤0”，正确；
②当0＜a＜1时，y=a^x为减函数，y=3-x²为开口向下的二次函数，两曲线有两个交点，函数f（x）=x²+a^x-3有两个零点，故②错误；
③由-

π

2

≤2x-

π

3

≤

π

2

得：-

π

12

≤x≤

5π

12

，即函数y=sin（2x-

π

3

）的一个单调增区间是[-

π

12

，

5π

12

]，即③正确；
④∵f（-x）=f（x），故y=f（x）为偶函数，
又当x＞0时，f′（x）＞0，
∴y=f（x）在区间（0，+∞）上单调递增，
由偶函数在对称区间上单调性相反知，y=f（x）在区间（-∞，0）上单调递减，即当x＜0时，f′（x）＜0，故④正确；
⑤∵y=m+

3

m

，
∴y′=1-

3

m2

，
∴当m∈（0，1]时，y′＜0，即函数y=m+

3

m

在区间（0，1]上单调递减，
∴当x=1时，y_min=1+3=4，故⑤错误；
综上所述，真命题的序号是①③④．
故答案为：①③④．

点评：本题考查命题的真假判断与应用，着重考查命题的否定、函数的零点、函数的单调性、奇偶性的应用，属于中档题．