题目内容
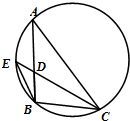 如图,圆内接△ABC的角平分线CD延长后交圆于一点E,ED=1,DC=4,BD=2,则AD=
如图,圆内接△ABC的角平分线CD延长后交圆于一点E,ED=1,DC=4,BD=2,则AD=考点:与圆有关的比例线段
专题:计算题,直线与圆
分析:根据相交弦定理,结合题中数据算出AD=2.再由CE平分∠ACB可得△EBD∽△ECB,利用比例线段加以计算,即可算出EB的长.
解答:
解:∵ED=1,DC=4,BD=2,
∴根据相交弦定理,得AD•BD=CD•ED,即AD•2=4•1,解得AD=2.
又∵CE平分∠ACB,可得∠EBD=∠ECB=∠ACD
∴△EBD∽△ECB,可得
=
,即
=
,解之得EB=
故答案为:2,
∴根据相交弦定理,得AD•BD=CD•ED,即AD•2=4•1,解得AD=2.
又∵CE平分∠ACB,可得∠EBD=∠ECB=∠ACD
∴△EBD∽△ECB,可得
| EB |
| EC |
| ED |
| EB |
| EB |
| 5 |
| 1 |
| EB |
| 5 |
故答案为:2,
| 5 |
点评:本题给出圆满足的条件,求线段长.着重考查了相交弦定理、相似三角形的判定与性质等知识,属于中档题.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
由0,1,2,3,4这5个数字组成没有重复数字且个位上的数字不能为1的3位数共有( )
| A、28个 | B、36个 |
| C、39个 | D、42个 |
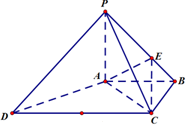 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=90°,且PA=AB=BC=
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=90°,且PA=AB=BC=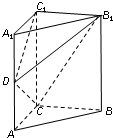 如图,在正三棱柱ABC-A1B1C1中,AA1=AB=2.
如图,在正三棱柱ABC-A1B1C1中,AA1=AB=2.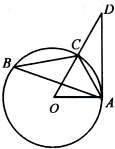 如图,已知△ABC内接于圆O,点D在OC的延长线上,AD是圆O的切线,若∠OAC=60°,AC=1,则AD的长为
如图,已知△ABC内接于圆O,点D在OC的延长线上,AD是圆O的切线,若∠OAC=60°,AC=1,则AD的长为