题目内容
已知抛物线y2=2px(p>0),过其焦点且斜率为-1的直线交抛物线于A、B两点,若线段AB的中点的纵坐标为-2,则该抛物线的准线方程为 .
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设A(x1,y1),B(x2,y2),由题设条件知直线AB的方程为x=-y+
,代入抛物线方程,得y2+2py-p2=0,由线段AB的中点的纵坐标为-2,推导出y1+y2=-2p=-4,由此能求出结果.
| p |
| 2 |
解答:
解:∵抛物线y2=2px(p>0),过其焦点且斜率为-1的直线交抛物线于A、B两点,
∴直线AB的方程为:y=-x+
,
∴x=-y+
,
把x=-y+
代入抛物线方程,
整理得y2+2py-p2=0,
设A(x1,y1),B(x2,y2),
则y1+y2=-2p,
∵线段AB的中点的纵坐标为-2,
∴y1+y2=-4,
∴p=2,
∴抛物线方程为y2=4x,
∴该抛物线的准线方程为x=-1.
故答案为:x=-1.
∴直线AB的方程为:y=-x+
| p |
| 2 |
∴x=-y+
| p |
| 2 |
把x=-y+
| p |
| 2 |
整理得y2+2py-p2=0,
设A(x1,y1),B(x2,y2),
则y1+y2=-2p,
∵线段AB的中点的纵坐标为-2,
∴y1+y2=-4,
∴p=2,
∴抛物线方程为y2=4x,
∴该抛物线的准线方程为x=-1.
故答案为:x=-1.
点评:本题考查抛物线的准线方程的求法,是中档题,解题时要熟练掌握抛物线的简单性质.

练习册系列答案
相关题目
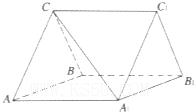 如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.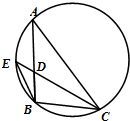 如图,圆内接△ABC的角平分线CD延长后交圆于一点E,ED=1,DC=4,BD=2,则AD=
如图,圆内接△ABC的角平分线CD延长后交圆于一点E,ED=1,DC=4,BD=2,则AD=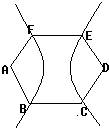 如图,正六边形ABCDEF的两个顶点A、D为双曲线的焦点,其余四个顶点都在双曲线上,则该双曲线的离心率为
如图,正六边形ABCDEF的两个顶点A、D为双曲线的焦点,其余四个顶点都在双曲线上,则该双曲线的离心率为