题目内容
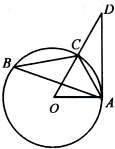 如图,已知△ABC内接于圆O,点D在OC的延长线上,AD是圆O的切线,若∠OAC=60°,AC=1,则AD的长为
如图,已知△ABC内接于圆O,点D在OC的延长线上,AD是圆O的切线,若∠OAC=60°,AC=1,则AD的长为考点:与圆有关的比例线段
专题:计算题,直线与圆
分析:由∠OAC=60°证出△OAC是等边三角形,可得OA=AC=1,∠O=60°.再利用切线的性质定理,在Rt△OAD中利用锐角三角函数的定义,即可算出AD之长.
解答:
解:∵OC=OA,∠OAC=60°,
∴△OAC是等边三角形,可得OA=AC=1,∠O=60°.
又∵AD与圆O相切于点A,∴OA⊥AD,
Rt△OAD中,tan∠O=
=
,可得AD=
OA=
.
故答案为:
∴△OAC是等边三角形,可得OA=AC=1,∠O=60°.
又∵AD与圆O相切于点A,∴OA⊥AD,
Rt△OAD中,tan∠O=
| AD |
| AO |
| 3 |
| 3 |
| 3 |
故答案为:
| 3 |
点评:本题给出圆的切线,求线段AD的长度.着重考查了等边三角形的判定与性质、圆的切线的性质定理和锐角三角函数的定义等知识,属于中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
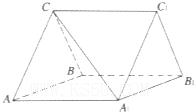 如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.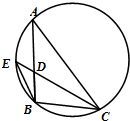 如图,圆内接△ABC的角平分线CD延长后交圆于一点E,ED=1,DC=4,BD=2,则AD=
如图,圆内接△ABC的角平分线CD延长后交圆于一点E,ED=1,DC=4,BD=2,则AD=