题目内容
正方体ABCD-A1B1C1D1中,A1B与平面BB1D1D所成的角为 .
考点:直线与平面所成的角
专题:综合题,空间角
分析:连接A1C1交B1D1于O,连接OB,说明∠ABO为A1B与平面BB1D1D所成的角,然后求解即可.
解答:
 解:连接A1C1交B1D1于O,连接OB,
解:连接A1C1交B1D1于O,连接OB,
因为B1D1⊥A1C1,A1C1⊥BB1,所以A1C1⊥平面BB1D1D,
所以∠ABO为A1B与平面BB1D1D所成的角,
设正方体棱长为1,所以A1O=
,A1B=
,
所以sin∠ABO=
=
,
所以∠ABO=30°.
故答案为:30°.
 解:连接A1C1交B1D1于O,连接OB,
解:连接A1C1交B1D1于O,连接OB,因为B1D1⊥A1C1,A1C1⊥BB1,所以A1C1⊥平面BB1D1D,
所以∠ABO为A1B与平面BB1D1D所成的角,
设正方体棱长为1,所以A1O=
| ||
| 2 |
| 2 |
所以sin∠ABO=
| ||||
|
| 1 |
| 2 |
所以∠ABO=30°.
故答案为:30°.
点评:本题考查直线与平面所成角的求法,找出直线与平面所成角是解题的关键,考查计算能力.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
二进制数101110(2)转化为八进制数为( )
| A、45(8) |
| B、56(8) |
| C、67(8) |
| D、78(8) |
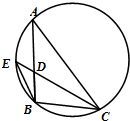 如图,圆内接△ABC的角平分线CD延长后交圆于一点E,ED=1,DC=4,BD=2,则AD=
如图,圆内接△ABC的角平分线CD延长后交圆于一点E,ED=1,DC=4,BD=2,则AD=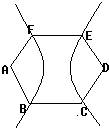 如图,正六边形ABCDEF的两个顶点A、D为双曲线的焦点,其余四个顶点都在双曲线上,则该双曲线的离心率为
如图,正六边形ABCDEF的两个顶点A、D为双曲线的焦点,其余四个顶点都在双曲线上,则该双曲线的离心率为