题目内容

函数y=3x-
2
x
在[1，2]上的最大值为
 
．
考点：函数的值域
专题：常规题型,函数的性质及应用
分析：本题考查的是利用基本初等函数的单调性求函数的最值．
解答： 解：因为函数y=3x和函数y=-
2
x
，在区间[1，2]上单调递增，
所以函数y=3x-
2
x
在区间[1，2]上也是单调递增，又f（2）=5，所以最大值为5．
故答案为：5．
点评：根据两个增函数的和为增函数的性质，很容易就能求出函数的最大值．
练习册系列答案
相关题目
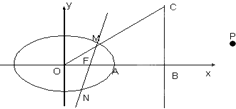已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）经过点T(
2
，-
6
2
)，其离心率为
1
2
，右顶点为A，右焦点为F（c，0），直线x=
a2
c
与x轴交于B，过点F的直线l与椭圆交于不同的两点M、N，点P为点M关于直线x=
a2
c
的对称点．
（1）求椭圆C的方程；
（2）求证：N、B、P三点共线；
（3）求△BNM的面积的最大值．
如图，多面体ABCDEF中，BA，BC，BE两两垂直，且AB∥EF，CD∥BE，AB=BE=2，BC=CD=EF=1．
（Ⅰ）若点G在线段AB上，且BG=3GA，求证：CG∥平面ADF；
（Ⅱ）求直线DE与平面ADF所成的角的正弦值．
过圆x2+y2=1上一点Q作圆的一点切线L，则L和抛物线y=
1
4
x2+1有公共点的概率是多少？
将6人分成甲、乙、丙三组，一组1人，一组2人，一组3人，共有分法
 
种．
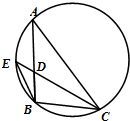如图，圆内接△ABC的角平分线CD延长后交圆于一点E，ED=1，DC=4，BD=2，则AD=
 
；EB=
 
．
曲线C是平面内与两个定点F1（-1，0）、F2（1，0）的距离的积等于常数a2（a＞1）的点的轨迹．给出下列四个结论：
①曲线C过坐标原点；
②曲线C关于坐标原点对称；
③若点P在曲线C上，则△F1PF2的面积不大于
1
2
a2；
④若点P在曲线C上，则P到原点的距离不小于
a2-1
．
其中正确命题序号是
 
．
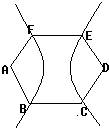如图，正六边形ABCDEF的两个顶点A、D为双曲线的焦点，其余四个顶点都在双曲线上，则该双曲线的离心率为
 
．
春节期间，某单位安排甲、乙、丙三人于正月初一至初五值班，每人至少值班一天，且每人均不能连续值班两天，其中初二不安排甲值班，则共有
 
种不同的值班安排方案．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网