题目内容
19.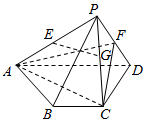 如图.四棱锥P-ABCD中,底面ABCD为等腰梯形,BC∥AD,平面PCD⊥平面ABCD,E.F,G分别是PA,PD,PC的中点,PF⊥PG,AB=BC=CD=$\frac{1}{2}$AD.
如图.四棱锥P-ABCD中,底面ABCD为等腰梯形,BC∥AD,平面PCD⊥平面ABCD,E.F,G分别是PA,PD,PC的中点,PF⊥PG,AB=BC=CD=$\frac{1}{2}$AD.(1)求证:EG∥平面ACF;
(2)求证:PE⊥PF.
分析 (1)由中位线定理可得EG∥AC,故而EG∥平面ACF;
(2)利用等腰三角形的性质求出cos∠ADC,利用余弦定理求出AC,根据勾股定理的逆定理得出AC⊥CD,于是AC⊥平面PCD,得出AC⊥PF,结合PF⊥PG得出PF⊥平面PAC,故而PE⊥PF.
解答  证明:(1)∵E,G分别是PA,PC的中点,
证明:(1)∵E,G分别是PA,PC的中点,
∴EG∥AC,又EG?平面ACF,AC?平面ACF,
∴EG∥平面ACF.
(2)过C作CM⊥AD于M,则DM=$\frac{1}{2}$(AD-BC)=$\frac{1}{2}BC$=$\frac{1}{2}CD$.
∴cos∠ADC=$\frac{DM}{CD}=\frac{1}{2}$.
设BC=1,则CD=1,AD=2,在△ACD中使用余弦定理得AC2=AD2+CD2-2AD•CD•cos∠ADC=3.
∴AC2+CD2=AD2,即AC⊥CD.
∵平面PCD⊥平面ABCD,平面PCD∩平面ABCD=CD,AC?平面ABCD,
∴AC⊥平面PCD,∵PF?平面PCD,
∴PF⊥AC,
又∵PF⊥PG,AC?平面PAC,PG?平面PAC,AC∩PG=C,
∴PF⊥平面PAC,∵PE?平面PAC,
∴PF⊥PE.
点评 本题考查了线面平行的判定,线面垂直的判定,面面垂直的性质,属于中档题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
9.命题p:若a<b,则ac2<bc2;命题q:?x0>0,使得x0-1-lnx0=0,则下列命题为真命题的是( )
| A. | p∧q | B. | p∨(¬q) | C. | (¬p)∧q | D. | (¬p)∧(¬q) |
10.已知两条异面直线a,b上分别有5个点和8个点,则这13个点可以确定不同的平面个数为( )
| A. | 40 | B. | 16 | C. | 13 | D. | 10 |
11.设$\overrightarrow a$=(1,2),$\overrightarrow b$=(x,y),$\overrightarrow c$=$\overrightarrow a$+$\overrightarrow b$.若$\overrightarrow b$⊥$\overrightarrow c$,则点(x,y)的轨迹方程为( )
| A. | (x-$\frac{1}{2}$)2+(y-1)2=$\frac{5}{4}$ | B. | ${(x+\frac{1}{2})^2}+{(y-1)^2}=\frac{5}{4}$ | C. | ${(x-\frac{1}{2})^2}+{(y+1)^2}=\frac{5}{4}$ | D. | ${(x+\frac{1}{2})^2}+{(y+1)^2}=\frac{5}{4}$ |