题目内容
10．已知两条异面直线a，b上分别有5个点和8个点，则这13个点可以确定不同的平面个数为（ ）| A． | 40 | B． | 16 | C． | 13 | D． | 10 |
分析 根据直线及直线外一点可以确定一个平面，对这13个点所确定的平面个数分析判断即可．
解答 解：根据直线与直线外一点可以确定一个平面，得：
a上任一点与直线b确定一平面，共5个，
b上任一点与直线a确定一平面，共8个，
由加法原理得共有5+8=13个．
故选：C．
点评 本题主要考查了平面的基本性质及推论的应用问题，是基础题目．
练习册系列答案
阅读快车系列答案
相关题目
20．已知x，y满足约束条件$\left\{\begin{array}{l}x-y+1≥0\\ x+y-2≥0\\ x≤2\end{array}\right.$，则目标函数z=2x-y的最大值为（ ）
| A． | -$\frac{1}{2}$ | B． | 1 | C． | 4 | D． | 5 |
18．已知椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{{b}^{2}}$=1（b＞0）与椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1有相同的焦点，则实数b的值为（ ）
| A． | 2 | B． | 3 | C． | 2$\sqrt{3}$ | D． | 4 |
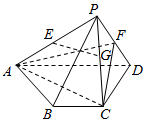如图．四棱锥P-ABCD中，底面ABCD为等腰梯形，BC∥AD，平面PCD⊥平面ABCD，E．F，G分别是PA，PD，PC的中点，PF⊥PG，AB=BC=CD=$\frac{1}{2}$AD．
20．直线l1：3x-4y+2=0与直线l2：4x+3y-1=0的位置关系是（ ）
| A． | 垂直 | B． | 平行 | C． | 相交但不垂直 | D． | 重合 |