题目内容
9.求和:Sn=$\frac{1}{2}$+$\frac{3}{{2}^{2}}$+$\frac{5}{{2}^{3}}$+$\frac{7}{{2}^{4}}$+…+$\frac{2n-1}{{2}^{n}}$.分析 利用“错位相减法”与等比数列的前n项和公式即可得出.
解答 解:Sn=$\frac{1}{2}$+$\frac{3}{{2}^{2}}$+$\frac{5}{{2}^{3}}$+$\frac{7}{{2}^{4}}$+…+$\frac{2n-1}{{2}^{n}}$,
∴$\frac{1}{2}$Sn=$\frac{1}{{2}^{2}}+\frac{3}{{2}^{3}}$+…+$\frac{2n-3}{{2}^{n}}$+$\frac{2n-1}{{2}^{n+1}}$,
∴$\frac{1}{2}$Sn=$\frac{1}{2}+$2$(\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+…+\frac{1}{{2}^{n}})$-$\frac{2n-1}{{2}^{n+1}}$=2×$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$-$\frac{1}{2}$-$\frac{2n-1}{{2}^{n+1}}$=$\frac{3}{2}$-$\frac{2n+3}{{2}^{n+1}}$,
∴Sn=3-$\frac{2n+3}{{2}^{n}}$.
点评 本题考查了“错位相减法”与等比数列的前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
20.直线l1:3x-4y+2=0与直线l2:4x+3y-1=0的位置关系是( )
| A. | 垂直 | B. | 平行 | C. | 相交但不垂直 | D. | 重合 |
4.已知数列{an}满足a1=1,an•an+1=2n,n∈N,Sn是数列{an}的前n项和,则S10等于( )
| A. | 63 | B. | 93 | C. | 126 | D. | 1023 |
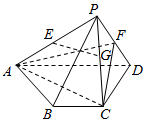 如图.四棱锥P-ABCD中,底面ABCD为等腰梯形,BC∥AD,平面PCD⊥平面ABCD,E.F,G分别是PA,PD,PC的中点,PF⊥PG,AB=BC=CD=$\frac{1}{2}$AD.
如图.四棱锥P-ABCD中,底面ABCD为等腰梯形,BC∥AD,平面PCD⊥平面ABCD,E.F,G分别是PA,PD,PC的中点,PF⊥PG,AB=BC=CD=$\frac{1}{2}$AD.