题目内容
11.设$\overrightarrow a$=(1,2),$\overrightarrow b$=(x,y),$\overrightarrow c$=$\overrightarrow a$+$\overrightarrow b$.若$\overrightarrow b$⊥$\overrightarrow c$,则点(x,y)的轨迹方程为( )| A. | (x-$\frac{1}{2}$)2+(y-1)2=$\frac{5}{4}$ | B. | ${(x+\frac{1}{2})^2}+{(y-1)^2}=\frac{5}{4}$ | C. | ${(x-\frac{1}{2})^2}+{(y+1)^2}=\frac{5}{4}$ | D. | ${(x+\frac{1}{2})^2}+{(y+1)^2}=\frac{5}{4}$ |
分析 根据条件可求出向量$\overrightarrow{c}$的坐标,而由$\overrightarrow{b}⊥\overrightarrow{c}$便可得到$\overrightarrow{b}•\overrightarrow{c}=0$,这样进行向量数量积的坐标运算即可得出点(x,y)的轨迹方程.
解答 解:由已知得$\overrightarrow c=\overrightarrow a+\overrightarrow b=(1+x,2+y)$;
又$\overrightarrow b⊥\overrightarrow c$;
∴$\overrightarrow{b}•\overrightarrow{c}=0$;
即x(1+x)+y(2+y)=0,化简得:
${(x+\frac{1}{2})^2}+{(y+1)^2}=\frac{5}{4}$.
故选:D.
点评 考查向量坐标的加法运算,向量垂直的充要条件,以及向量数量积的坐标运算,配方法的运用.

练习册系列答案
相关题目
20.直线l1:3x-4y+2=0与直线l2:4x+3y-1=0的位置关系是( )
| A. | 垂直 | B. | 平行 | C. | 相交但不垂直 | D. | 重合 |
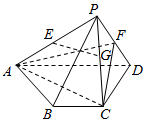 如图.四棱锥P-ABCD中,底面ABCD为等腰梯形,BC∥AD,平面PCD⊥平面ABCD,E.F,G分别是PA,PD,PC的中点,PF⊥PG,AB=BC=CD=$\frac{1}{2}$AD.
如图.四棱锥P-ABCD中,底面ABCD为等腰梯形,BC∥AD,平面PCD⊥平面ABCD,E.F,G分别是PA,PD,PC的中点,PF⊥PG,AB=BC=CD=$\frac{1}{2}$AD.