题目内容
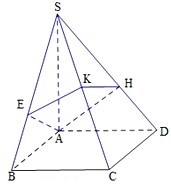如图，ABCD为正方形，过A作线段SA⊥面ABCD，又过A作与SC垂直的平面交SB、SC、SD于E、K、H，求证：E是点A在直线SB上的射影．考点：直线与平面垂直的性质
专题：空间位置关系与距离
分析：根据线面垂直的判定定理以及性质定理进行证明即可．
解答：
证明：∵SA⊥ABCD，∴BC⊥SA，
∵ABCD为正方形，∴BC⊥AB，
∵SA∩AB=A，∴BC⊥SAB，
∴EA⊥BC，
∵SC⊥AEKH，∴EA⊥SC，
∵BC∩SC=C，
∴EA⊥SBC，
∴EA⊥SB，
∴E是点A在直线SB上的射影．
∵ABCD为正方形，∴BC⊥AB，
∵SA∩AB=A，∴BC⊥SAB，
∴EA⊥BC，
∵SC⊥AEKH，∴EA⊥SC，
∵BC∩SC=C，
∴EA⊥SBC，
∴EA⊥SB，
∴E是点A在直线SB上的射影．
点评：本题考查了线面垂直的判定定理，性质定理，是一道基础题．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
设两直线l1：x+y
+b=0，l2：xsinθ+y
-a=0，θ∈（π，
π），则直线l1和l2的位置关系是（ ）
| 1-cosθ |
| 1+cosθ |
| 3 |
| 2 |
| A、平行 | B、平行或重合 |
| C、垂直 | D、相交但不一定垂直 |
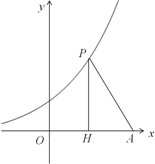如图，已知点A（10，0），直线x=t（0＜t＜10）与函数y=e2x+1的图象交于点P，与x轴交于点H，记△APH的面积为f（t）．