题目内容
设两直线l1:x+y
+b=0,l2:xsinθ+y
-a=0,θ∈(π,
π),则直线l1和l2的位置关系是( )
| 1-cosθ |
| 1+cosθ |
| 3 |
| 2 |
| A、平行 | B、平行或重合 |
| C、垂直 | D、相交但不一定垂直 |
考点:直线的一般式方程与直线的平行关系
专题:直线与圆
分析:由题意求出两直线的斜率,由斜率之积等于-1得答案.
解答:
解:∵θ∈(π,
π),
∴cosθ≠±1,
∴l1的斜率为-
,l2的斜率为-
,
则-
•(-
)=
=
=-1,
∴直线l1和l2的位置关系是垂直.
故选:C.
| 3 |
| 2 |
∴cosθ≠±1,
∴l1的斜率为-
| 1 | ||
|
| sinθ | ||
|
则-
| 1 | ||
|
| sinθ | ||
|
| sinθ |
| |sinθ| |
| sinθ |
| -sinθ |
∴直线l1和l2的位置关系是垂直.
故选:C.
点评:本题考查了由直线的一般式方程判断直线的位置关系,关键是分析出直线的斜率存在,是基础题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
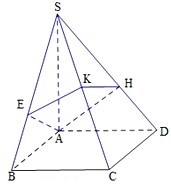 如图,ABCD为正方形,过A作线段SA⊥面ABCD,又过A作与SC垂直的平面交SB、SC、SD于E、K、H,求证:E是点A在直线SB上的射影.
如图,ABCD为正方形,过A作线段SA⊥面ABCD,又过A作与SC垂直的平面交SB、SC、SD于E、K、H,求证:E是点A在直线SB上的射影.