题目内容
定义在(0,+∞)上的函数f(x)满足:对任意x∈(0,+∞)恒有2f(x+2)=f(x)成立;当x∈(0,2]时,f(x)=-|1-x|+1.给出以下命题:
①f(5)=
;
②当x∈(2,4]时,f(x)∈[0,
];
③令g(x)-f(x)=k(x-1),若函数g(x)恰有三个零点,则实数k的取值范围是(
,
);
④?x0∈(0,+∞),使f(x0)>(
) x0-1成立.
其中所有真命题的序号是 .
①f(5)=
| 1 |
| 4 |
②当x∈(2,4]时,f(x)∈[0,
| 1 |
| 2 |
③令g(x)-f(x)=k(x-1),若函数g(x)恰有三个零点,则实数k的取值范围是(
| 1 |
| 16 |
| 1 |
| 4 |
④?x0∈(0,+∞),使f(x0)>(
| ||
| 2 |
其中所有真命题的序号是
考点:命题的真假判断与应用
专题:计算题,作图题,函数的性质及应用,简易逻辑
分析:①注意到2f(x+2)=f(x),f(5)=
f(3)=
f(1)=
,
②注意到2f(x+2)=f(x),f(x)=
f(x-2)=-
|3-x|+
,从而求范围,
③作出函数的图象,函数g(x)恰有三个零点可化为函数f(x)与直线y=-k(x-1)有三个不同的交点,从而求解,
④作出函数的图象,由图象可得.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
②注意到2f(x+2)=f(x),f(x)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
③作出函数的图象,函数g(x)恰有三个零点可化为函数f(x)与直线y=-k(x-1)有三个不同的交点,从而求解,
④作出函数的图象,由图象可得.
解答:
 解:∵2f(x+2)=f(x),∴f(x)=
解:∵2f(x+2)=f(x),∴f(x)=
f(x-2),
∴f(5)=
f(3)=
f(1)=
,故①正确;
∵x∈(2,4],∴x-2∈(0,2];
∴f(x)=
f(x-2)=-
|3-x|+
,
∵0≤|3-x|≤1,∴f(x)∈[0,
],故②正确;
函数g(x)恰有三个零点可化为
函数f(x)与直线y=-k(x-1)有三个不同的交点,
故
<-k<
,
故-
<k<-
,故③不正确;
由y=(
)x-1=2
,
作图如下,

f(x)的图象始终在y=2
图象的下方,
故④不成立.
故答案为:①②.
 解:∵2f(x+2)=f(x),∴f(x)=
解:∵2f(x+2)=f(x),∴f(x)=| 1 |
| 2 |
∴f(5)=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
∵x∈(2,4],∴x-2∈(0,2];
∴f(x)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵0≤|3-x|≤1,∴f(x)∈[0,
| 1 |
| 2 |
函数g(x)恰有三个零点可化为
函数f(x)与直线y=-k(x-1)有三个不同的交点,
故
| 0.25 |
| 4 |
| 0.5 |
| 2 |
故-
| 1 |
| 4 |
| 1 |
| 16 |
由y=(
| ||
| 2 |
| 1-x |
| 2 |
作图如下,

f(x)的图象始终在y=2
| 1-x |
| 2 |
故④不成立.
故答案为:①②.
点评:本题考查了函数的性质与函数的图象的作法,同时考查了命题真假性的判断,属于难题.

练习册系列答案
相关题目
 如图是长方体被一平面所截后得到的几何体,四边形EFGH为截面,长方形ABCD为长方体的底面,则四边形EFGH的形状为( )
如图是长方体被一平面所截后得到的几何体,四边形EFGH为截面,长方形ABCD为长方体的底面,则四边形EFGH的形状为( )| A、梯形 | B、平行四边形 |
| C、梯形或平行四边形 | D、不能确定 |
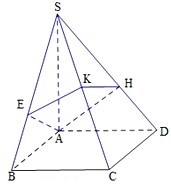 如图,ABCD为正方形,过A作线段SA⊥面ABCD,又过A作与SC垂直的平面交SB、SC、SD于E、K、H,求证:E是点A在直线SB上的射影.
如图,ABCD为正方形,过A作线段SA⊥面ABCD,又过A作与SC垂直的平面交SB、SC、SD于E、K、H,求证:E是点A在直线SB上的射影.