题目内容
已知正六边形ABCDEF的中心在坐标原点,外接圆半径为2,顶点AD在x轴上,求以A、D为焦点,且过点E的双曲线方程.
考点:双曲线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:如图所示,设双曲线的方程为
-
=1(a,b>0).由题意可得c=2,E(1,
).把E(1,
)代入双曲线的方程可得
-
=1,又c2=a2+b2.联立解得即可.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 3 |
| 1 |
| a2 |
| 3 |
| b2 |
解答:
解:如图所示,
设双曲线的方程为
-
=1(a,b>0).
由题意可得c=2,E(1,
).
把E(1,
)代入双曲线的方程可得
-
=1,又c2=a2+b2.
联立解得a2=4-2
,b2=2
.
∴双曲线的方程为:
-
=1.

设双曲线的方程为
| x2 |
| a2 |
| y2 |
| b2 |
由题意可得c=2,E(1,
| 3 |
把E(1,
| 3 |
| 1 |
| a2 |
| 3 |
| b2 |
联立解得a2=4-2
| 3 |
| 3 |
∴双曲线的方程为:
| x2 | ||
4-2
|
| y2 | ||
2
|
点评:本题考查了双曲线的标准方程及其性质、正六边形的性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若直线a⊥直线b,直线b⊥平面β,则a与β的关系是( )
| A、a⊥β | B、a∥β |
| C、a?β | D、a?β或a∥β |
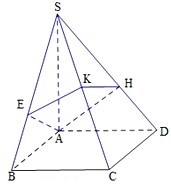 如图,ABCD为正方形,过A作线段SA⊥面ABCD,又过A作与SC垂直的平面交SB、SC、SD于E、K、H,求证:E是点A在直线SB上的射影.
如图,ABCD为正方形,过A作线段SA⊥面ABCD,又过A作与SC垂直的平面交SB、SC、SD于E、K、H,求证:E是点A在直线SB上的射影.