题目内容
已知双曲线的中心S在原点、焦点在x轴上，离心率e=
，直线3x-3y+5=0上的点与双曲线S的右焦点距离最小值等于4
，求S的方程．
| ||
| 2 |
| 3 |
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：由题意，设S的方程
-
=1，从而得到方程组
，解出代回即可．
| x2 |
| a2 |
| y2 |
| b2 |
|
解答：
解：由题意，设S的方程
-
=1，则其右焦点的坐标为（c，0），
故可得
，
解得，c=
，a2=
，b2=
，
故S的方程为
-
=1．
| x2 |
| a2 |
| y2 |
| b2 |
故可得
|
解得，c=
12
| ||
| 3 |
2(12
| ||
| 27 |
(12
| ||
| 27 |
故S的方程为
| 27x2 | ||
2•(12
|
| 27y2 | ||
(12
|
点评：本题考查了圆锥曲线的定义，化简比较困难，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
已知全集U={1，2，3，4，5，6.7}，A={2，4，6}，B={3，5，6，7}．则A∩（∁UB）等于（ ）
| A、{2，4，6} |
| B、{2，4} |
| C、{1，3，5} |
| D、{2，5} |
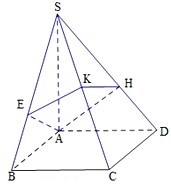如图，ABCD为正方形，过A作线段SA⊥面ABCD，又过A作与SC垂直的平面交SB、SC、SD于E、K、H，求证：E是点A在直线SB上的射影．