题目内容
判断E:y=
x+2与2x2+3y2=6是否有公共点,若有,求交点坐标,若无,求出椭圆上的点到E的距离最大值.
| ||
| 6 |
考点:椭圆的简单性质
专题:圆锥曲线中的最值与范围问题
分析:根据题意,由直线方程与椭圆方程联立,利用判别式判断方程组无解,得直线与椭圆无交点;
设椭圆的任意一点P,求出点P到直线E的距离d的最大值即可.
设椭圆的任意一点P,求出点P到直线E的距离d的最大值即可.
解答:
解:由题意得,
,
消去y,得2x2+3(
x+2)2=6;
整理得3x2+4
x+12=0,
∵△=(4
)2-4×3×12=-48<0,
∴方程组无解,即直线与椭圆无交点;
又椭圆方程可化为
+
=1,
设椭圆上的任意一点P(
cosα,
sinα),
则点P到直线E:
x-y+2=0的距离是
d=
=
≤
=
,
∴椭圆上的点到E的距离最大值是
.
|
消去y,得2x2+3(
| ||
| 6 |
整理得3x2+4
| 6 |
∵△=(4
| 6 |
∴方程组无解,即直线与椭圆无交点;
又椭圆方程可化为
| x2 |
| 3 |
| y2 |
| 2 |
设椭圆上的任意一点P(
| 3 |
| 2 |
则点P到直线E:
| ||
| 6 |
d=
|
| ||||||||
|
|
| ||||
|
2+
| ||||
|
2
| ||||
| 7 |
∴椭圆上的点到E的距离最大值是
2
| ||||
| 7 |
点评:本题考查了直线与椭圆方程的应用问题,解题时应利用代数法与几何法相结合,利用椭圆的参数方程进行解答,是中档题目.

练习册系列答案
相关题目
△ABC的内角A,B,C的对边分别为a,b,c,a2=bc,且c=2b,则cosA=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知全集U={1,2,3,4,5,6.7},A={2,4,6},B={3,5,6,7}.则A∩(∁UB)等于( )
| A、{2,4,6} |
| B、{2,4} |
| C、{1,3,5} |
| D、{2,5} |
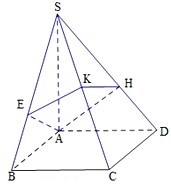 如图,ABCD为正方形,过A作线段SA⊥面ABCD,又过A作与SC垂直的平面交SB、SC、SD于E、K、H,求证:E是点A在直线SB上的射影.
如图,ABCD为正方形,过A作线段SA⊥面ABCD,又过A作与SC垂直的平面交SB、SC、SD于E、K、H,求证:E是点A在直线SB上的射影.