题目内容
在△ABC中,a,b,c分别为角A,B,C的对边,且4sin2
-cos2A=
.
(Ⅰ)求角A的大小;
(Ⅱ)若a=
且a≤b,求b-
c的取值范围.
| B+C |
| 2 |
| 7 |
| 2 |
(Ⅰ)求角A的大小;
(Ⅱ)若a=
| 3 |
| 1 |
| 2 |
考点:正弦定理,三角函数中的恒等变换应用
专题:解三角形
分析:(Ⅰ)把已知等式利用二倍角公式化简整理可求得cosA的值,进而求得A.
(Ⅱ)利用正弦定理分别表示出b和c,进而利用角的正弦表示出b-
c进而根据三角函数的性质和B的范围求得答案.
(Ⅱ)利用正弦定理分别表示出b和c,进而利用角的正弦表示出b-
| 1 |
| 2 |
解答:
解:(Ⅰ)∵A+B+C=π,
∴sin
=sin
=cos
,
∵4sin2
-cos2A=4cos2
-cos2A=2(1+cosA)-(2cos2A-1)=
∴整理得(2cosA-1)2=0解得cosA=
,
∴A=
(Ⅱ)∵
=
=
=2,
∴b=2sinB,c=2sinC
∴b-
c=2sinB-sinC=2sinB-sin(
-B)=
sinB-
cosB=
sin(B-
)
∵a≤b,
∴
≤B<
,
∴
≤B-
<
∴b-
c=
sin(B-
)∈[
,
)
∴sin
| B+C |
| 2 |
| π-A |
| 2 |
| A |
| 2 |
∵4sin2
| B+C |
| 2 |
| A |
| 2 |
| 7 |
| 2 |
∴整理得(2cosA-1)2=0解得cosA=
| 1 |
| 2 |
∴A=
| π |
| 3 |
(Ⅱ)∵
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
∴b=2sinB,c=2sinC
∴b-
| 1 |
| 2 |
| 2π |
| 3 |
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| π |
| 6 |
∵a≤b,
∴
| π |
| 3 |
| 2 |
| 3 |
∴
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
∴b-
| 1 |
| 2 |
| 3 |
| π |
| 6 |
| ||
| 2 |
| 3 |
点评:本题主要考查了正弦定理的应用,三角函数的性质,二倍角公式等知识点.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
已知cosα=
,α∈(370°,520°),则α等于( )
| 1 |
| 2 |
| A、390° | B、420° |
| C、450° | D、480° |
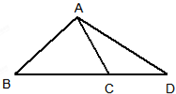 如图,在△ABC中,内角A,B,C的对边分别是a,b,c,且bsinA=acosB,D是BC延长线上的一点,AC=5,AD=7,CD=3.
如图,在△ABC中,内角A,B,C的对边分别是a,b,c,且bsinA=acosB,D是BC延长线上的一点,AC=5,AD=7,CD=3.