题目内容
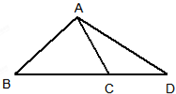 如图,在△ABC中,内角A,B,C的对边分别是a,b,c,且bsinA=acosB,D是BC延长线上的一点,AC=5,AD=7,CD=3.
如图,在△ABC中,内角A,B,C的对边分别是a,b,c,且bsinA=acosB,D是BC延长线上的一点,AC=5,AD=7,CD=3.(1)求∠ACD的大小和∠ACD的面积;
(2)求AB的长.
考点:正弦定理
专题:解三角形
分析:(1)利用余弦定理求得∠ACD,进而根据三角形面积公式求得答案.
(2)利用正弦定理把已知等式的边转化成角的正弦,整理求得B,进而根据正弦定理求得AB.
(2)利用正弦定理把已知等式的边转化成角的正弦,整理求得B,进而根据正弦定理求得AB.
解答:
解:(1)在△ABC中,∵cos∠ACD=
=-
,
∴∠ACD=120°,
∴S△ACD=
AC•CD•sin∠ACD=
×5×3×
=
.
(2)∵bsinA=acosB,
∴由正弦定理得:sinBsinA=sinAcosB,sinA>0,
∴sinB=cosB,
∴B=
,
∵∠ACB=
,
=
,
∴AB=
×
=
.
| 25+9-49 |
| 2×5×3 |
| 1 |
| 2 |
∴∠ACD=120°,
∴S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
15
| ||
| 4 |
(2)∵bsinA=acosB,
∴由正弦定理得:sinBsinA=sinAcosB,sinA>0,
∴sinB=cosB,
∴B=
| π |
| 4 |
∵∠ACB=
| π |
| 3 |
| AB | ||
sin
|
| AC | ||
sin
|
∴AB=
| 5 | ||||
|
| ||
| 2 |
5
| ||
| 2 |
点评:本题主要考查了正弦定理和余弦定理的运用.在解三角形问题中往往把正弦定理和余弦定理考查.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
设f(x)在x=2处有导数,则
=( )
| lim |
| △x→0 |
| f(2+△x)-f(2-△x) |
| 2△x |
| A、2f′(2) | ||
B、
| ||
| C、f′(2) | ||
| D、4f′(2) |