题目内容
在△ABC中,角A、B、C所对的边分别为a、b、c,且5sin
=cosC+2.
(1)求角C的大小;
(2)若
+1=
,c=2,求边a的长.
| C |
| 2 |
(1)求角C的大小;
(2)若
| tanA |
| tanB |
4
| ||
| 3b |
考点:正弦定理,同角三角函数基本关系的运用
专题:解三角形
分析:(1)利用二倍角公式对原式进行化简整理,可求得sin
,进而求得C.
(2)利用同角三角函数关系,把正切化成正弦和余弦化简整理可求得cosA的值,进而求得sinA的值,最后利用正弦定理求得a.
| C |
| 2 |
(2)利用同角三角函数关系,把正切化成正弦和余弦化简整理可求得cosA的值,进而求得sinA的值,最后利用正弦定理求得a.
解答:
解:(1)∵5sin
=cosC+2,
∴5sin
=1-2sin2
+2,(sin
+3)(2sin
-1)=0,
∴sin
=
,sin
=-3(不合题意)
∴∠C=
.
(2)∵
+1=
,c=2,
∴
+1=
=
=
∵
=
,
∴
=
∴
=
∴
=
=
,
∴cosA=
,
∴sinA=
,
由正弦定理得:
=
,a=
=
.
| C |
| 2 |
∴5sin
| C |
| 2 |
| C |
| 2 |
| C |
| 2 |
| C |
| 2 |
∴sin
| C |
| 2 |
| 1 |
| 2 |
| C |
| 2 |
∴∠C=
| π |
| 3 |
(2)∵
| tanA |
| tanB |
4
| ||
| 3b |
∴
| sinA•cosB |
| cosA•sinB |
| sin(A+B) |
| cosAsinB |
| ||||
| cosAsinB |
4
| ||
| 3b |
∵
| b |
| sinB |
| c |
| sinC |
∴
| c |
| b |
| sinC |
| sinB |
∴
4
| ||
| 3b |
4
| ||
| 3sinB |
∴
| ||||
| cosAsinB |
4
| ||
| 3b |
4
| ||
| 3sinB |
∴cosA=
| ||
| 4 |
∴sinA=
| ||
| 4 |
由正弦定理得:
| c |
| sinC |
| a |
| sinA |
| csinA |
| sinC |
| ||
| 3 |
点评:本题主要考查正弦定理的应用,三角函数恒等变换的应用.考查了学生基础知识的综合运用.

练习册系列答案
相关题目
今有5位同学排成一排照相,其中甲、乙两人必须相邻,则不同的排法共有( )
| A、48种 | B、24种 |
| C、8种 | D、20种 |
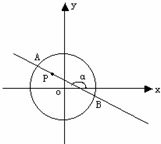 圆x2+y2=8内有一点P(-1,2),AB为过点P且倾斜角为α的弦,
圆x2+y2=8内有一点P(-1,2),AB为过点P且倾斜角为α的弦,