题目内容

△ABC中，AB=
3
，AC=1，∠C=60°，则△ABC的面积等于
 
．
考点：余弦定理,三角形的面积公式
专题：解三角形
分析：利用余弦定理可得BC，再利用三角形的面积计算公式即可得出．
解答： 解：由余弦定理可得：AB2=AC2+BC2-2AC•BCcosC，
∴3=1+BC2-2•BC•cos60°，
化为BC2-BC-2=0，
解得BC=2．
∴△ABC的面积S=
1
2
CB•CA•sinC=
1
2
×2×1×sin60°=
3
2
．
故答案为：
3
2
．
点评：本题考查了余弦定理、三角形的面积计算公式，属于基础题．
练习册系列答案
相关题目
P为椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）上一点，F1为它的一个焦点，求证：以PF1为直径的圆与以长轴为直径的圆相切．
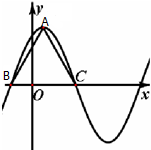已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
π
2
）是某简谐运动的函数解析式，如图为该函数在一个周期内的图象，A为图象的最高点，坐标为A（
2
3
，2
3
）、B、C为图象与x轴的交点，且为正三角形．
（1）求该简谐运动的函数解析式；
（2）若f（x0）=
8
3
5
，且x0∈（-
10
3
，
2
3
），求f（x0+2）的值．
长方体ABCD-A1B1C1D1中，AB=BC=1，BB1=
2
，设点A关于直线BD1的对称点为P，则P与C1两点之间的距离为（　　）
A、1
B、
2
C、
3
3
D、
3
2
已知函数f（x）=a+
2
2x-1
为奇函数．
（Ⅰ）求实数a的值；
（Ⅱ）证明|f（x）|＞1．
若2x-3y+z=3，则x2+（y-1）2+z2的最小值为
 
．
已知在△ABC中，a=3，b=
3
，sinA=
6
3
，求c．
已知函数f（x）的定义域为D，若存在闭区间[a，b]⊆D，使得函数f（x）满足：①f（x）在[a，b]内是单调函数；②f（x）在[a，b]上的值域为[2a，2b]，则称区间[a，b]为y=f（x）的“倍值区间”，下列函数中存在“倍值区间”的有
 
．
①f（x）=2x（x∈R）
②f（x）=x2（x≥0）
③f（x）=ex（x∈R）
④f（x）=lnx（x＞0）
一次数学测验后某班成绩均在（20，100]区间内，统计后画出的频率分布直方图如图，如分数在
（60，70]分数段内有9人．则此班级的总人数为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网