题目内容
14. 某加油站工作人员根据以往该加油站的销售情况,绘制了该加油站日销售量的频率分布直方图,如图所示.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
某加油站工作人员根据以往该加油站的销售情况,绘制了该加油站日销售量的频率分布直方图,如图所示.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.(1)求未来3天内,连续2天日销售量不低于40吨,另一天的日销售量低于40吨的概率;
(2)用ξ表示未来3天日销售量不低于40吨的天数,求随机变量ξ的数学期望.
分析 (1)由频率分布直方图求出日销售量不低于40吨的频率为0.4,记未来3天内,第i天日销售量不低于40吨的事件为Ai(i=1,2,3),则P(Ai)=0.4,未来3天内,连续2天日销售量不低于40吨,另一天的日销售量低于40吨包含两个互斥事件:${A}_{1}{A}_{2}\overline{{A}_{3}}$和$\overline{{A}_{1}}{A}_{2}{A}_{3}$,由此能求出未来3天内,连续2天日销售量不低于40吨,另一天的日销售量低于40吨的概率.
(2)ξ的可能取值为0,1,2,3,且ξ~B(3,0.4),由此能求出ξ的数学期望.
解答 解:(1)由频率分布直方图知:
日销售量不低于40吨的频率为:10×(0.025+0.015)=0.4,
记未来3天内,第i天日销售量不低于40吨的事件为Ai(i=1,2,3),
则P(Ai)=0.4,
未来3天内,连续2天日销售量不低于40吨,另一天的日销售量低于40吨包含两个互斥事件:
${A}_{1}{A}_{2}\overline{{A}_{3}}$和$\overline{{A}_{1}}{A}_{2}{A}_{3}$,
∴未来3天内,连续2天日销售量不低于40吨,另一天的日销售量低于40吨的概率为:
P(${A}_{1}{A}_{2}\overline{{A}_{3}}$∪$\overline{{A}_{1}}{A}_{2}{A}_{3}$)=P(${A}_{1}{A}_{2}\overline{{A}_{3}}$)+P($\overline{{A}_{1}}{A}_{2}{A}_{3}$)
=0.4×0.4×(1-0.4)+(1-0.4)×0.4×0.4=0.192.
(2)ξ的可能取值为0,1,2,3,
P(ξ=0)=(1-0.4)2=0.216,
P(ξ=1)=${C}_{3}^{1}×0.4×(1-0.4)^{2}$=0.432,
P(ξ=2)=${C}_{3}^{2}×0.{4}^{2}×(1-0.4)$=0.288,
P(ξ=3)=0.43=0.064,
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | 0.216 | 0.432 | 0.288 | 0.064 |
点评 本题考查概率的求法,考查离散型随机变量的数学期望的求法,是中档题,解题时要认真审题,注意频率分布直方图的性质及二项分布的性质的合理运用.

 名校课堂系列答案
名校课堂系列答案| A. | [-$\frac{π}{2}$+2kπ,π+2kπ],k∈Z | B. | [-$\frac{π}{2}$+3kπ,π+3kπ],k∈Z | ||
| C. | [π+2kπ,$\frac{5π}{2}$+2kπ],k∈Z | D. | [π+3kπ,$\frac{5π}{2}$+3kπ],k∈Z |
| A. | {1,2} | B. | {1,2,3,4} | C. | {1,2,3} | D. | {1,2,4} |
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $-\frac{3}{2}$ |
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
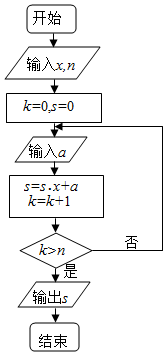 秦九韶是我国南宋时期著名的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为3,每次输入a的值均为4,输出s的值为484,则输入n的值为( )
秦九韶是我国南宋时期著名的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为3,每次输入a的值均为4,输出s的值为484,则输入n的值为( )