题目内容
6.已知数列{an}的前n项和Sn=2an-1,则满足$\frac{a_n}{n}≤2$的正整数n的集合为( )| A. | {1,2} | B. | {1,2,3,4} | C. | {1,2,3} | D. | {1,2,4} |
分析 数列{an}的前n项和Sn=2an-1,∴n=1时,a1=2a1-1,解得a1.n≥2时,an=Sn-Sn-1,化为:an=2an-1,利用等比数列的不等式可得an=2n-1,不等式$\frac{a_n}{n}≤2$即2n-2≤n,即可得出.
解答 解:数列{an}的前n项和Sn=2an-1,∴n=1时,a1=2a1-1,解得a1=1.
n≥2时,an=Sn-Sn-1=2an-1-(2an-1-1),化为:an=2an-1,
∴数列{an}是等比数列,公比为2.
∴an=2n-1,
不等式$\frac{a_n}{n}≤2$即2n-2≤n,
当n=1,2,3,4时,满足上述不等式.
n≥5时,上述不等式不成立.
∴满足$\frac{a_n}{n}≤2$的正整数n的集合为{1,2,3,4}.
故选:B.
点评 本题考查了数列递推关系、数列通项公式、不等式的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.已知函数f(x)=Asin(ωx+φ)$(A>0,|φ|<\frac{π}{2})$的图象(部分)如图所示,则$f(-\frac{1}{2})$=( )
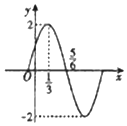

| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\sqrt{3}$ | D. | $\sqrt{3}$ |
11.命题“ax2-2ax+3>0恒成立”是假命题,则实数a的取值范围是( )
| A. | 0<a<3 | B. | a<0或a≥3 | C. | a<0或a>3 | D. | a≤0或a≥3 |
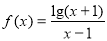 的定义域是( )
的定义域是( ) 某加油站工作人员根据以往该加油站的销售情况,绘制了该加油站日销售量的频率分布直方图,如图所示.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
某加油站工作人员根据以往该加油站的销售情况,绘制了该加油站日销售量的频率分布直方图,如图所示.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.