题目内容
2.在多项式(1+2x)6(1+y)5的展开式中,xy3项的系数为120.分析 利用二项式展开式的通项公式即可得出.
解答 解:根据题意(1+2x)6(1+y)5=$(1+{∁}_{6}^{1}•2x+…)$$({y}^{5}+{∁}_{5}^{1}{y}^{4}+{∁}_{5}^{2}{y}^{3}+…)$,
∴xy3的系数为${∁}_{6}^{1}×2×{∁}_{5}^{2}$=120,
故答案为:120.
点评 本题考查了二项式定理的应用,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
11.设命题$p:?x∈R,{x^2}-x+\frac{1}{4}≥0$,则¬p为( )
| A. | $?x∈R,x_{\;}^2-x+\frac{1}{4}≥0$ | B. | $?x∈R,x_{\;}^2-x+\frac{1}{4}<0$ | ||
| C. | $?x∈R,x_{\;}^2-x+\frac{1}{4}≤0$ | D. | $?x∈R,{x^2}-x+\frac{1}{4}<0$ |
17.若复数$z=\frac{2}{{1+{i^3}}}$,其中i为虚数单位,则复数z的虚部是( )
| A. | -1 | B. | -i | C. | 1 | D. | i |
11.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | 16π | B. | 8π | C. | $\frac{16}{3}$π | D. | $\frac{8}{3}$π |
10.若不等式组$\left\{\begin{array}{l}{x+y-3≥0}\\{y≤kx+3}\\{0≤x≤2}\end{array}\right.$表示的平面区域是一个锐角三角形,则实数k的取值范围是( )
| A. | (-∞,-1) | B. | (-1,0) | C. | (1,+∞) | D. | (0,1) |
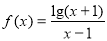 的定义域是( )
的定义域是( ) 某加油站工作人员根据以往该加油站的销售情况,绘制了该加油站日销售量的频率分布直方图,如图所示.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
某加油站工作人员根据以往该加油站的销售情况,绘制了该加油站日销售量的频率分布直方图,如图所示.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.