题目内容
19．若双曲线C：x2-$\frac{y^2}{b^2}$=1（b＞0）的离心率为2，则b=（ ）| A． | 1 | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | 2 |
分析 由a=1，c=$\sqrt{1+{b}^{2}}$，离心率为e=$\frac{c}{a}$=$\sqrt{1+{b}^{2}}$=，解得：b=$\sqrt{3}$．
解答 解：双曲线C：x2-$\frac{y^2}{b^2}$=1（b＞0）焦点在x轴上，a=1，c=$\sqrt{1+{b}^{2}}$，
∴离心率为e=$\frac{c}{a}$=$\sqrt{1+{b}^{2}}$=，解得：b=$\sqrt{3}$，
故选C．
点评 本题考查双曲线的简单几何性质，离心率公式，属于基础题．
练习册系列答案
相关题目
11．已知$a={log_2}\sqrt{2}$，$b={log_{\sqrt{3}}}2$，c=log35，则（ ）
| A． | c＞b＞a | B． | b＞c＞a | C． | a＞b＞c | D． | c＞a＞b |
11．命题“ax2-2ax+3＞0恒成立”是假命题，则实数a的取值范围是（ ）
| A． | 0＜a＜3 | B． | a＜0或a≥3 | C． | a＜0或a＞3 | D． | a≤0或a≥3 |
某加油站工作人员根据以往该加油站的销售情况，绘制了该加油站日销售量的频率分布直方图，如图所示．将日销售量落入各组的频率视为概率，并假设每天的销售量相互独立．
11．设命题$p：?x∈R，{x^2}-x+\frac{1}{4}≥0$，则￢p为（ ）
| A． | $?x∈R，x_{\;}^2-x+\frac{1}{4}≥0$ | B． | $?x∈R，x_{\;}^2-x+\frac{1}{4}＜0$ | ||
| C． | $?x∈R，x_{\;}^2-x+\frac{1}{4}≤0$ | D． | $?x∈R，{x^2}-x+\frac{1}{4}＜0$ |
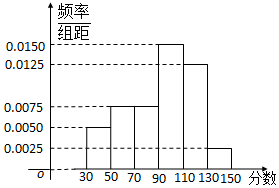从某校高三上学期期末数学考试成绩中，随机抽取了60名学生的成绩得到如图所示的频率分布直方图：