题目内容
10.设函数f(x)(x∈R)满足f(x-π)=f(x)+sinx,当0≤x≤π,f(x)=1时,则$f({-\frac{13π}{6}})$=( )| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $-\frac{3}{2}$ |
分析 利用条件以及诱导公式,求得要求式子的值.
解答 解:∵f(x-π)=f(x)+sinx,当0≤x≤π,f(x)=1时,
则$f({-\frac{13π}{6}})$=f(-$\frac{7π}{6}$-π)=f(-$\frac{7π}{6}$)+sin(-$\frac{7π}{6}$)=f(-$\frac{π}{6}$-π)+sin(-$\frac{7π}{6}$)
=f(-$\frac{π}{6}$)+sin(-$\frac{π}{6}$)+sin(-$\frac{7π}{6}$)=f($\frac{5π}{6}$-π)+sin(-$\frac{π}{6}$)-sin$\frac{7π}{6}$
=f($\frac{5π}{6}$)+sin$\frac{5π}{6}$+sin(-$\frac{π}{6}$)+sin$\frac{π}{6}$=1+$\frac{1}{2}$-$\frac{1}{2}$+$\frac{1}{2}$=$\frac{3}{2}$,
故选:C.
点评 本题主要考查新定义,诱导公式的应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知函数f(x)=Asin(ωx+φ)$(A>0,|φ|<\frac{π}{2})$的图象(部分)如图所示,则$f(-\frac{1}{2})$=( )
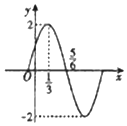

| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\sqrt{3}$ | D. | $\sqrt{3}$ |
5.设偶函数f(x)满足f(x)=2x-4(x≥0),则满足f(a-2)>0的实数a的取值范围为( )
| A. | (2,+∞) | B. | (4,+∞) | C. | (0,4) | D. | (-∞,0)∪(4,+∞) |
1.执行如图所示的程序框图,输出S的值为( )


| A. | 6 | B. | 2log23+1 | C. | 2log23+3 | D. | log23+1 |
17.若复数$z=\frac{2}{{1+{i^3}}}$,其中i为虚数单位,则复数z的虚部是( )
| A. | -1 | B. | -i | C. | 1 | D. | i |
 某加油站工作人员根据以往该加油站的销售情况,绘制了该加油站日销售量的频率分布直方图,如图所示.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
某加油站工作人员根据以往该加油站的销售情况,绘制了该加油站日销售量的频率分布直方图,如图所示.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.