题目内容
3.棱台的两底面面积为S1、S2,中截面(过各棱中点的面积)面积为S0,那么( )| A. | $2\sqrt{S_0}=\sqrt{S_1}+\sqrt{S_2}$ | B. | ${S_0}=\sqrt{{S_1}{S_2}}$ | C. | 2S0=S1+S2 | D. | S02=2S1S2 |
分析 不妨设这个棱台为三棱台,设棱台的高为2h,上部三棱锥的高为a,根据相似比的性质,能求出结果.
解答 解:不妨设这个棱台为三棱台,设棱台的高为2h,上部三棱锥的高为a,
则根据相似比的性质,得:
$\left\{\begin{array}{l}{(\frac{a}{a+2h})^{2}=\frac{{S}_{2}}{{S}_{1}}}\\{(\frac{a}{a+h})^{2}=\frac{{S}_{2}}{{S}_{0}}}\end{array}\right.$,
解得$2\sqrt{{S}_{0}}$=$\sqrt{{S}_{1}}$+$\sqrt{{S}_{2}}$.
故选:A.
点评 本题考查棱台的两底面面积和中截面(过各棱中点的面积)面积间的关系式的判断,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
8.已知函数f(x)=$\sqrt{3}$sin2x-cos2x+1,下列结论中错误的是( )
| A. | f(x)的图象关于($\frac{π}{12}$,1)中心对称 | B. | f(x)在($\frac{5π}{12}$,$\frac{11π}{12}$)上单调递减 | ||
| C. | f(x)的图象关于x=$\frac{π}{3}$对称 | D. | f(x)的最大值为3 |
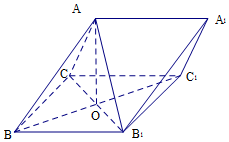 如图,在三棱柱ABC-A1B1C1中,侧面BB1C1C 为菱形,B1C与BC1交于点O,AO⊥平面BB1C1C
如图,在三棱柱ABC-A1B1C1中,侧面BB1C1C 为菱形,B1C与BC1交于点O,AO⊥平面BB1C1C 某公司13个部门接受的快递的数量如茎叶图所示,则这13个部门接受的快递的数量的中位数为10.
某公司13个部门接受的快递的数量如茎叶图所示,则这13个部门接受的快递的数量的中位数为10.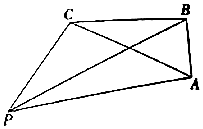 如图,有一码头P和三个岛屿A,B,C,PC=30$\sqrt{3}$n mile,PB=90n mile,AB=30n mile,∠PCB=120°,∠ABC=90°.
如图,有一码头P和三个岛屿A,B,C,PC=30$\sqrt{3}$n mile,PB=90n mile,AB=30n mile,∠PCB=120°,∠ABC=90°.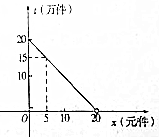 2016年9月,第22届鲁台经贸洽谈会在潍坊鲁台会展中心举行,在会展期间某展销商销售一种商品,根据市场调查,每件商品售价x(元)与销量t(万元)之间的函数关系如图所示,又知供货价格与销量呈反比,比例系数为20.(注:每件产品利润=售价-供货价格)
2016年9月,第22届鲁台经贸洽谈会在潍坊鲁台会展中心举行,在会展期间某展销商销售一种商品,根据市场调查,每件商品售价x(元)与销量t(万元)之间的函数关系如图所示,又知供货价格与销量呈反比,比例系数为20.(注:每件产品利润=售价-供货价格)