题目内容
15.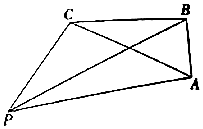 如图,有一码头P和三个岛屿A,B,C,PC=30$\sqrt{3}$n mile,PB=90n mile,AB=30n mile,∠PCB=120°,∠ABC=90°.
如图,有一码头P和三个岛屿A,B,C,PC=30$\sqrt{3}$n mile,PB=90n mile,AB=30n mile,∠PCB=120°,∠ABC=90°.(1)求B,C两个岛屿间的距离;
(2)某游船拟载游客从码头P前往这三个岛屿游玩,然后返回码头P,问该游船应按何路线航行,才能使得总航程最短?求出最短航程.
分析 (1)设BC=xn mile,则由余弦定理可求B,C两个岛屿间的距离;
(2)由题意,AC=60,PA=30$\sqrt{7}$,即可得出结论.
解答 解:(1)设BC=xn mile,则由余弦定理可得$8100=2700+{x}^{2}-60\sqrt{3}x•(-\frac{1}{2})$,
∴x=30$\sqrt{3}$n mile;
(2)由题意,AC=60,PA=30$\sqrt{7}$,
∴PA+AB+BC+CP=60$\sqrt{3}$+30+30$\sqrt{7}$(n mile).
点评 本题考查利用数学知识解决实际问题,考查余弦定理的运用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.棱台的两底面面积为S1、S2,中截面(过各棱中点的面积)面积为S0,那么( )
| A. | $2\sqrt{S_0}=\sqrt{S_1}+\sqrt{S_2}$ | B. | ${S_0}=\sqrt{{S_1}{S_2}}$ | C. | 2S0=S1+S2 | D. | S02=2S1S2 |
20.已知i是虚数单位,复数z=a+i(a∈R)满足z2+z=1-3i,则a=( )
| A. | -2 | B. | -2或1 | C. | 2或-1 | D. | 1 |
5.已知过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点F(-c,0)和虚轴端点E的直线交双曲线的右支于点P,若E为线段FP的中点,则该双曲线的离心率为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{5}+1}{2}$ | D. | $\sqrt{5}$+1 |