题目内容
19.设ω>0,将函数f(x)=$\sqrt{2}$cosωx的图象向左平移$\frac{π}{2}$个单位,若所得的图象与原图象重合,则正数ω的最小值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 首先通过平移变换得到函数的解析式:g(x)=$\sqrt{2}$cos(ωx+$\frac{π}{2}$ω),进一步利用函数图象重合,令ωx=2kπ+ωx+$\frac{π}{2}$ω,(k∈Z)即可解得正数ω的最小值.
解答 解:函数f(x)=$\sqrt{2}$cosωx(ω>0)向左平移$\frac{π}{2}$个单位后得到:
g(x)=$\sqrt{2}$cos[ω(x+$\frac{π}{2}$)]=$\sqrt{2}$cos(ωx+$\frac{π}{2}$ω)所得的图象与原图象重合,
令:ωx=2kπ+ωx+$\frac{π}{2}$ω,(k∈Z)
即:ω=-4k,(k∈Z)
当k=-1时,正数ω的最小值为4.
故选:D.
点评 本题主要考查了函数y=Asin(ωx+φ)的图象变换,余弦函数的图象和性质,考查了数形结合思想的应用,属于基础题.

练习册系列答案
相关题目
9.已知椭圆C:$\frac{{x}^{2}}{4}$+y2=1的左、右顶点分别为A、B,点M为C上不同于A、B的任意一点,则直线MA、MB的斜率之积为( )
| A. | $\frac{1}{4}$ | B. | -4 | C. | -$\frac{1}{4}$ | D. | 4 |
10.已知函数$f(x)=\frac{3x}{a}-2{x^2}+lnx$,其中a为常数.
(1)若a=1,求函数f(x)的单调区间;
(2)若函数f(x)在区间[1,2]上为单调增函数,求a的取值范围.
(1)若a=1,求函数f(x)的单调区间;
(2)若函数f(x)在区间[1,2]上为单调增函数,求a的取值范围.
3.棱台的两底面面积为S1、S2,中截面(过各棱中点的面积)面积为S0,那么( )
| A. | $2\sqrt{S_0}=\sqrt{S_1}+\sqrt{S_2}$ | B. | ${S_0}=\sqrt{{S_1}{S_2}}$ | C. | 2S0=S1+S2 | D. | S02=2S1S2 |
20.已知i是虚数单位,复数z=a+i(a∈R)满足z2+z=1-3i,则a=( )
| A. | -2 | B. | -2或1 | C. | 2或-1 | D. | 1 |
1.过点P(1,2),并且在两坐标轴上的截距相等的直线方程是( )
| A. | x+y-3=0或x-2y=0 | B. | x+y-3=0或2x-y=0 | ||
| C. | x-y+1=0或x+y-3=0 | D. | x-y+1=0或2x-y=0 |
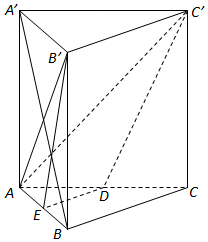 如图所示,直三棱柱ABC-A′B′C中,∠ABC=90°,AB=BC=BB′=2,D为底棱AC的中点.
如图所示,直三棱柱ABC-A′B′C中,∠ABC=90°,AB=BC=BB′=2,D为底棱AC的中点.