题目内容
13.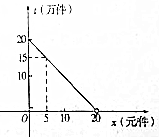 2016年9月,第22届鲁台经贸洽谈会在潍坊鲁台会展中心举行,在会展期间某展销商销售一种商品,根据市场调查,每件商品售价x(元)与销量t(万元)之间的函数关系如图所示,又知供货价格与销量呈反比,比例系数为20.(注:每件产品利润=售价-供货价格)
2016年9月,第22届鲁台经贸洽谈会在潍坊鲁台会展中心举行,在会展期间某展销商销售一种商品,根据市场调查,每件商品售价x(元)与销量t(万元)之间的函数关系如图所示,又知供货价格与销量呈反比,比例系数为20.(注:每件产品利润=售价-供货价格)(1)求售价15元时的销量及此时的供货价格;
(2)当销售价格为多少时总利润最大,并求出最大利润.
分析 (1)每件商品售价x(元)与销量t(万件)之间的函数关系为t=20-x(0≤x≤20),设价格为y,则y=$\frac{20}{t}$,即可求售价15元时的销量及此时的供货价格;
(2)总利润L=(x-$\frac{20}{t}$)t=xt-20=x(20-x)-20≤$(\frac{x+20-x}{2})^{2}$-20=80,可得结论.
解答 解:(1)每件商品售价x(元)与销量t(万件)之间的函数关系为t=20-x(0≤x≤20),
设价格为y,则y=$\frac{20}{t}$,x=15时,t=5万件,y=4万元;
(2)总利润L=(x-$\frac{20}{t}$)t=xt-20=x(20-x)-20≤$(\frac{x+20-x}{2})^{2}$-20=80,
当且仅当x=10元时总利润最大,最大利润80万元.
点评 此题考查了一次函数与二次函数的知识,考查学生利用数学知识解决实际问题的能力,属于中档题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
3.棱台的两底面面积为S1、S2,中截面(过各棱中点的面积)面积为S0,那么( )
| A. | $2\sqrt{S_0}=\sqrt{S_1}+\sqrt{S_2}$ | B. | ${S_0}=\sqrt{{S_1}{S_2}}$ | C. | 2S0=S1+S2 | D. | S02=2S1S2 |
1.过点P(1,2),并且在两坐标轴上的截距相等的直线方程是( )
| A. | x+y-3=0或x-2y=0 | B. | x+y-3=0或2x-y=0 | ||
| C. | x-y+1=0或x+y-3=0 | D. | x-y+1=0或2x-y=0 |
18.抛物线x=2y2的焦点坐标是( )
| A. | (1,0) | B. | ($\frac{1}{2}$,0) | C. | ($\frac{1}{8}$,0) | D. | (0,$\frac{1}{8}$) |
5.已知过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点F(-c,0)和虚轴端点E的直线交双曲线的右支于点P,若E为线段FP的中点,则该双曲线的离心率为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{5}+1}{2}$ | D. | $\sqrt{5}$+1 |
2.执行如图的程序框图.输出的x的值是( )


| A. | 2 | B. | 14 | C. | 11 | D. | 8 |
3.设Sn为数列{an}的前n项和,a3=6且Sn+1=3Sn,则a1+a5等于( )
| A. | 12 | B. | $\frac{164}{3}$ | C. | 55 | D. | $\frac{170}{3}$ |
