题目内容
8.已知函数f(x)=$\sqrt{3}$sin2x-cos2x+1,下列结论中错误的是( )| A. | f(x)的图象关于($\frac{π}{12}$,1)中心对称 | B. | f(x)在($\frac{5π}{12}$,$\frac{11π}{12}$)上单调递减 | ||
| C. | f(x)的图象关于x=$\frac{π}{3}$对称 | D. | f(x)的最大值为3 |
分析 利用辅助角公式将函数进行化简,结合三角函数的单调性,最值性,对称性的性质分别进行判断即可.
解答 解:f(x)=$\sqrt{3}$sin2x-cos2x+1=2sin(2x-$\frac{π}{6}$)+1,
A.当x=$\frac{π}{12}$时,sin(2x-$\frac{π}{6}$)=0,则f(x)的图象关于($\frac{π}{12}$,1)中心对称,故A正确,
B.由2kπ+$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$,k∈Z,得kπ+$\frac{π}{3}$≤x≤kπ+$\frac{5π}{6}$,k∈Z,
当k=0时,函数的递减区间是[$\frac{π}{3}$,$\frac{5π}{6}$],故B错误,
C.当x=$\frac{π}{3}$时,2x-$\frac{π}{6}$=2×$\frac{π}{3}$-$\frac{π}{6}$=$\frac{π}{2}$,则f(x)的图象关于x=$\frac{π}{3}$对称,故C正确,
D.当2sin(2x-$\frac{π}{6}$)=1时,函数取得最大值为2+1=3,故D正确,
故选:B
点评 本题主要考查与三角函数有关的命题的真假判断,利用辅助角公式将函数进行化简,结合三角函数的性质是解决本题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
6.已知函数$f(x)=\left\{\begin{array}{l}{2^x}+1,x≤1\\ 1-{log_2}x,x>1\end{array}\right.$,则满足不等式f(1-m2)>f(2m-2)的m的取值范围是( )
| A. | (-3,1) | B. | $(\frac{3}{2},+∞)$ | C. | (-3,1)∪$(\frac{3}{2},+∞)$ | D. | $(-3,\frac{3}{2})$ |
3.棱台的两底面面积为S1、S2,中截面(过各棱中点的面积)面积为S0,那么( )
| A. | $2\sqrt{S_0}=\sqrt{S_1}+\sqrt{S_2}$ | B. | ${S_0}=\sqrt{{S_1}{S_2}}$ | C. | 2S0=S1+S2 | D. | S02=2S1S2 |
20.已知i是虚数单位,复数z=a+i(a∈R)满足z2+z=1-3i,则a=( )
| A. | -2 | B. | -2或1 | C. | 2或-1 | D. | 1 |
17.设向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1,|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{3}$,$\overrightarrow{a}$•($\overrightarrow{a}$+$\overrightarrow{b}$)=0,则|2$\overrightarrow{a}$-$\overrightarrow{b}$|=( )
| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{3}$ |
18.抛物线x=2y2的焦点坐标是( )
| A. | (1,0) | B. | ($\frac{1}{2}$,0) | C. | ($\frac{1}{8}$,0) | D. | (0,$\frac{1}{8}$) |
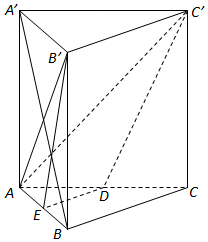 如图所示,直三棱柱ABC-A′B′C中,∠ABC=90°,AB=BC=BB′=2,D为底棱AC的中点.
如图所示,直三棱柱ABC-A′B′C中,∠ABC=90°,AB=BC=BB′=2,D为底棱AC的中点.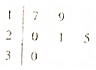 某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.