题目内容
2．已知f（x）为R上的偶函数，当x＞0时，f（x）=log6x，则f（-4）+f（9）=2．分析 根据函数奇偶性的性质进行转化求解即可．
解答 解：∵f（x）为R上的偶函数，当x＞0时，f（x）=log6x，
∴f（-4）+f（9）=f（4）+f（9）=log64+log69=log6（4×9）=log636=2，
故答案为：2．
点评 本题主要考查函数值的计算，根据函数奇偶性的性质进行转化是解决本题的关键．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
12．已知集合A={x∈Z|（x+2）（x-1）＜0}，B={-2，-1}，那么A∪B等于（ ）
| A． | {-1} | B． | {-2，-1} | C． | {-2，-1，0} | D． | {-2，-1，0，1} |
10．已知函数$f（x）=\frac{3x}{a}-2{x^2}+lnx$，其中a为常数．
（1）若a=1，求函数f（x）的单调区间；
（2）若函数f（x）在区间[1，2]上为单调增函数，求a的取值范围．
（1）若a=1，求函数f（x）的单调区间；
（2）若函数f（x）在区间[1，2]上为单调增函数，求a的取值范围．
17．
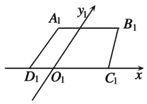如图，梯形A1B1C1D1是一平面图形ABCD的直观图（斜二测），若AD∥Oy，AB∥CD，A1B1=$\frac{3}{4}{C_1}{D_1}=3，{A_1}{D_1}$=1，则原平面图形ABCD的面积是（ ）
如图，梯形A1B1C1D1是一平面图形ABCD的直观图（斜二测），若AD∥Oy，AB∥CD，A1B1=$\frac{3}{4}{C_1}{D_1}=3，{A_1}{D_1}$=1，则原平面图形ABCD的面积是（ ）| A． | 14． | B． | 7 | C． | $14\sqrt{2}$ | D． | $7\sqrt{2}$ |
3．棱台的两底面面积为S1、S2，中截面（过各棱中点的面积）面积为S0，那么（ ）
| A． | $2\sqrt{S_0}=\sqrt{S_1}+\sqrt{S_2}$ | B． | ${S_0}=\sqrt{{S_1}{S_2}}$ | C． | 2S0=S1+S2 | D． | S02=2S1S2 |