题目内容
16.对于实数x,用[x]表示不超过x的最大整数,如[0.32]=0,[5.68]=5.若n为正整数,an=[$\frac{n}{4}$],Sn为数列{an}的前n项和,则S40=( )| A. | 190 | B. | 180 | C. | 170 | D. | 160 |
分析 an=[$\frac{n}{4}$],可得n=1,2,3时,an=0;n=4,5,6,7,an=1;n=8,9,10,11,an=2;…,n=36,37,38,39,an=9.n=40,an=10.即可得出.
解答 解:an=[$\frac{n}{4}$],可得n=1,2,3时,an=0;
n=4,5,6,7,an=1;
n=8,9,10,11,an=2;
n=12,13,14,15,an=3;
…,
n=36,37,38,39,an=9.
n=40,an=10.
则S40=0+4×(1+2+…+8+9)+10=$4×\frac{9×(1+9)}{2}$+10=190.
点评 本题考查了等差数列的求和公式、取整函数的性质,考查了分类讨论方法、推理能力与计算能力,属于中档题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
1.在正方体ABCD-A1B1C1D1中,与平面ACC1A1平行的棱共有( )
| A. | 2条 | B. | 3条 | C. | 4条 | D. | 6条 |
8.等比数列{an}中,a1=3,a8=9,函数f(x)=x(x-a1)(x-a2)…(x-a8),则f'(0)=( )
| A. | 36 | B. | 39 | C. | 312 | D. | 315 |
5.为了得到函数y=3cos2x,x∈R的图象,只需要把函数y=3cos(2x+$\frac{π}{5}$),x∈R的图象上所有的点( )
| A. | 向左平移$\frac{π}{5}$个单位长度 | B. | 向右平移$\frac{π}{5}$个单位长度 | ||
| C. | 向左平移$\frac{π}{10}$个单位长度 | D. | 向右平移$\frac{π}{10}$个单位长度 |
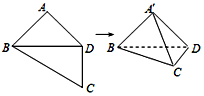 如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是(2)(3).
如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是(2)(3).