题目内容
11.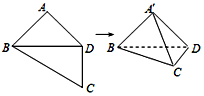 如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是(2)(3).
如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是(2)(3).(1)A′C⊥BD;
(2)∠BA′C=90°;
(3)四面体A′-BCD的体积为$\frac{1}{6}$.
分析 折叠前AB⊥AD,折叠后CD⊥平面A'BD,取BD的中点O,推导出A'O⊥平面BCD,OC不垂直于BD.由此能求出结果.
解答 解:∵折叠前AB=AD=1,BD=$\sqrt{2}$,即AB⊥AD,
折叠后平面A'BD⊥平面BCD,且CD⊥BD,
故CD⊥平面A'BD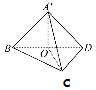 ,取BD的中点O,∵A'B=A'D,
,取BD的中点O,∵A'B=A'D,
∴A'O⊥BD.又平面A'BD⊥平面BCD,平面A'BD∩平面BCD=BD,
∴A'O⊥平面BCD.
∵CD⊥BD,
∴OC不垂直于BD.假设A'C⊥BD,
∵OC为A'C在平面BCD内的射影,
∴OC⊥BD,矛盾,∴A'C不垂直于BD,故A错误;
∵CD⊥BD,平面A'BD⊥平面BCD,
∴CD⊥平面A'BD,A'C在平面A'BD内的射影为A'D.
∵A'B=A'D=1,BD=$\sqrt{2}$,
∴A'B⊥A'D,A'B⊥A'C,∴∠BA′C=90°,故(2)正确;
∵A′C与平面A'BD不垂直,故A′C与BD不垂直,故(1)错误;
V${\;}_{{A}^{'}-BCD}$=V${\;}_{C-{A}^{'}BD}$=$\frac{1}{3}$${S}_{△{A}^{'}BD}$•CD=$\frac{1}{6}$,故(3)正确.
故答案为:(2)(3).
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目